, Maneli Mozaffarieh1 and Hans Bebie2
(1)
Department of Ophthalmology, University of Basel, Basel, Switzerland
(2)
Institute for Theoretical Physics, University of Bern, Bern, Switzerland
Abstract
In many chapters, we have had “light” as our central theme – as a phenomenon of nature, as our connection to the outer world, as an instrument for ophthalmological examinations, and as a tool for therapeutic interventions. In this chapter, we would like to discuss some concepts regarding the physics of matter that can be encountered frequently in practice. Since we do not wish to present the broad systematic physics of matter, we limit considerations to the fluid phase and explain some concepts, taking water as our example. However, water itself is also a topic. The more one deals with its properties, the more one gets the impression that this material was created to enable life and its development billions of years later.
In many chapters, we have had “light” as our central theme – as a phenomenon of nature, as our connection to the outer world, as an instrument for ophthalmological examinations, and as a tool for therapeutic interventions. In this chapter, we would like to discuss some concepts regarding the physics of matter that can be encountered frequently in practice. Since we do not wish to present the broad systematic physics of matter, we limit considerations to the fluid phase and explain some concepts, taking water as our example.1 However, water itself is also a topic. The more one deals with its properties, the more one gets the impression that this material was created to enable life and its development billions of years later.
Just like light, water is taken for granted – but where does the earth’s water as a compound of hydrogen and oxygen come from? As we know, according to the Big Bang model, hydrogen nuclei (protons), helium nuclei, and electrons were created in the very first minutes. When, after a million years, the cooling had progressed far enough, the nuclei and the electrons combined to form neutral hydrogen and helium atoms. Heavier elements, among them oxygen, arose only in fusion processes in massive stars and were hurled out into outer space by supernova explosions millions of years later. The materials of the solar system, including the elements of life on earth, originate from earlier star generations. Water arose in outer space – in the Orion cloud, visible to the naked eye, unimaginably large amounts of water have been discovered and its creation continues.
Ice, water, and steam consist of identical water molecules. The electrical forces between the charge distributions of adjacent molecules determine all the phenomena that we observe daily, such as crystalline bonding to form solid ice, the surface tension of water, the specific heat capacity of water,2 the energy necessary to melt ice or to evaporate water, melting and evaporation temperatures, the viscosity of water (internal friction), the expansion of water as a function of temperature, the solubility of other substances, and numerous additional subtle phenomena.
18.1 The Isolated Water Molecule
The structure of the water molecule is very well known. The distance between the two hydrogen nuclei (protons) from the oxygen nucleus amounts to 0.074 nm and the angle between the bonds of the oxygen nucleus to the protons is 104.5°. In principle, the properties of the ground state as well as of the excited states are predicted theoretically with absolute precision by quantum theory.3 The bonding energy manifests itself in oxyhydrogen (a mixture of O2 and H2) explosions; it must be introduced again to split the hydrogen from the oxygen.
One of the most important characteristics of the water molecule is its strong polarity due to the fact that the negative charges (electrons) are shifted with respect to the positive charges (nuclei). The side with the two H atoms has a net positive charge and the side beyond the O atom has a negative one. A very simplified but easily remembered model is sketched in Fig. 18.1. It shows the main features of the polar charge distribution.
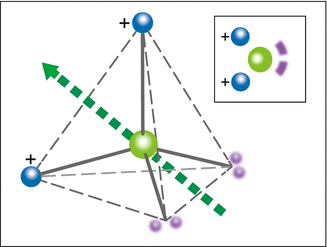

Fig. 18.1
A model of the polarity of the water molecule. The broken lines represent a tetrahedron (pyramid with six edges with the same length). The oxygen atom is located at its center of gravity and the two protons (nuclei of the H atoms – positive) in two of the corners. The two other corners of the tetrahedron are negatively charged and – in water or ice – they form bonds with the protons of other water molecules. The arrow indicates the electrical dipole moment. The four electrons of the covalent bonds of hydrogen to the oxygen as well as the two innermost oxygen electrons are not shown here. Insert: Simplified scheme representing the non-uniform charge distribution. Blue protons, purple electrons, green oxygen
18.2 The H-Bond in Ice and Water
The interaction between molecules in ice and water is dominated by H-bonds. The prototype can be studied in the water dimer (Fig. 18.2). The H-bond results mainly from the electrostatic attraction between a positive charge of the one molecule (proton) and a non-bonding electron pair of the other molecule. The strength of an H-bond amounts to approximately 0.2 eV, which is about 8 times the energy of thermal agitation.4 It is the energy needed to separate a pair of water molecules (mainly in evaporation).
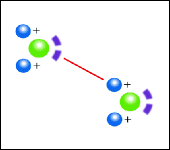

Fig. 18.2
The H-bond in the water dimer (symbolized by the red line) results from the electrostatic attraction between a proton of one molecule and electrons of the other. The distance between the oxygen nuclei amounts to about 0.3 nm
The structure of ice reflects the tetrahedral symmetry: each molecule has four nearest neighbors that form a tetrahedron (Fig. 18.3). In liquid water, each molecule is connected to its neighbors by, typically, three to four H-bonds. In a “snapshot,” only a minority of the molecules would be singles or dimers. Most are bound into smaller and larger networks with structures similar to that of ice. These clusters break apart permanently and then reform in other combinations. The motor of this dynamism is the thermal translation and rotation of the molecules. Thermal agitation sets the lifetimes of these bonds to an order of magnitude of 10-12 s. A measure of the mobility is so-called self-diffusion5: in water that is absolutely free of any currents, the random walk of a given molecule leads to a mean displacement of about 0.1 mm in a second, or 1 mm in a minute.


Fig. 18.3
Structure of ice. The green spheres represent the positions of the water molecules and the red links symbolize the H bonds. Each oxygen atom has four nearest neighbors; these form the corners of a tetrahedron. One obtains the occupied positions in a cubic raster: The center of every other cube is occupied. Four of the eight corners of each cube are occupied
18.3 Heat and Temperature
An alteration of the body temperature by 2 K (3.6 °F, 2 °C) has a strong and direct or indirect influence on life processes.6 For lifeless matter, this type of a temperature difference often means very little; for example, the pressure of a gas in a given volume changes by less than one percent. On the other hand, only a tiny temperature change across the freezing temperature suffices to change ice into liquid water and vice versa. What, then, is temperature – this variable that we seem to be so dependent on? What do the molecules of a stone in water have in common with water molecules when the stone takes on the water’s temperature? What do steam molecules and molecules of the boiling water have in common when both have the same temperature? Temperature is undoubtedly one of the more difficult concepts in physics.
It is only with noble gases that the question can easily be answered: the mean kinetic energy E kin of the atoms can be understood as the measure of the temperature. Not only are these two variables proportional to each other but the mean energy per atom for a given temperature is the same for all noble gases. This is expressed in the equation E kin = 3kT/2, where k is Boltzmann’s constant and T is the absolute temperature as expressed in Kelvin.7 The factor 3 corresponds to the three degrees of freedom and the three spatial dimensions. With molecular gases, comparable shares of rotation and, with higher temperatures, molecular vibrations are added in. Steam also obeys this rule: the mean thermal energy per molecule amounts to roughly 3kT. It is stored in the movements of the centers of gravity of the water molecules and their rotations, while additional degrees of freedom (intramolecular vibrations) are still little stimulated at the boiling temperature of water.
However, the simple proportionality between temperature and energy is true only for ideal gases. The relationship between heat energy in water and its temperature is shown in Fig. 18.4. It is not at all linear. The latent heat in the ice ↔ water transition stabilizes the climate and weather at temperatures around freezing. The latent heat of evaporation has its origin in the break-up of bonds between neighboring water molecules. This is the main mechanism for the cooling of our bodies through the evaporation of sweat. Water, for example, shows that we cannot simply identify temperature with energy per molecule, although it is true that the thermal energy of every system increases with rising temperatures. No doubt the reader will have noticed that we have left open the question as to what temperature is in terms of molecular physics.8
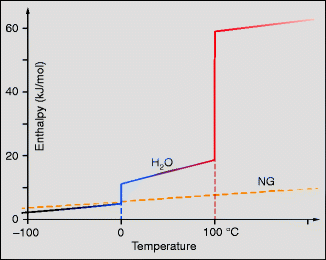

Fig. 18.4
Enthalpy (energy content at constant pressure) of water as well as that of a noble gas (NG) as a function of the temperature for 1 Mol at pressure of 1 bar. The two phase transitions (ice ↔ water, water ↔ steam) stabilize the temperature in that these also remain constant when the system takes in or gives off energy. In its liquid phase, water also stabilizes the temperature because the specific heat capacity is relatively large
18.4 Solubility of Gases: Partial Pressure
Water can contain dissolved gases. If we open a bottle of mineral water, CO2 is released. Blood serum contains dissolved N2, O2, and CO2. However, in comparison with the oxygen that is transported by the erythrocytes, the quantity of dissolved O2 in the blood is quite small. The basic situation is shown in Fig. 18.5: water in contact with a gas mixture (e.g., air). Here, the gases are present with their associated partial pressures, such as nitrogen in air with a partial pressure of 0.8 bar and oxygen with a partial pressure of 0.2 bar. If none of these is dissolved in water at the beginning, they gradually diffuse into it. With the growing concentration of the gases in water, a flow back into air builds up until equilibrium is attained between the flows of molecules in both directions through the water’s surface.
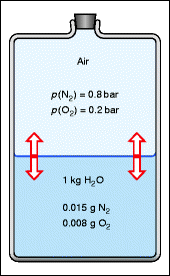

Fig. 18.5
Dissolved gases in water in equilibrium with a gas mixture. The dissolved quantities per kg of water can be derived from Table 18.1 by multiplying the solubility by the associated partial pressure, for example for N2 at 20 °C: 0.8∙0.019 = 0.015 g/kg
The dissolved quantity of a given gas is proportional to its partial pressure in the gas mixture that the water is in contact with. If the partial pressure is doubled, twice as much per unit time flows in through the water surface and the equilibrium is reached only when, due to the doubled concentration of the dissolved gases in the water, twice as much also flows out through the surface. Some concentrations in equilibrium are presented in Table 18.1, corresponding to a partial pressure of 1 bar.
Table 18.1
Some solubilities (in g of gases per 1 kg water) at a partial pressure of 1 bar. The dissolved quantities decrease with rising temperature. It is conspicuous that far more CO2 is dissolved than O2 or N2. The solubility of N2O (laughing gas) is close to that of CO2
Temperature | Solubility (g/kg H2O/1 bar) | |||
|---|---|---|---|---|
°C | °F | O2 | N2 | CO2 |
20 < div class='tao-gold-member'>
Only gold members can continue reading. Log In or Register to continue
Stay updated, free articles. Join our Telegram channel
Full access? Get Clinical Tree
 Get Clinical Tree app for offline access
Get Clinical Tree app for offline access

| ||||