, Maneli Mozaffarieh1 and Hans Bebie2
(1)
Department of Ophthalmology, University of Basel, Basel, Switzerland
(2)
Institute for Theoretical Physics, University of Bern, Bern, Switzerland
Abstract
In one of his Christmas lectures, Michael Faraday spoke about a classic source of light: a hot material (here, the flame of a candle) emitting light, known as thermal light. We find this process in a light bulb as well as in the radiation produced by the sun and stars or in the Olympic torch. In nature, other sources of light are rather rare, such as lightning, auroras, or the bioluminescence of a firefly. On the other hand, technology has made different (non-thermal) light sources available, e.g., fluorescent lamps, lasers, and light emitting diodes.
In one of his Christmas lectures,1 Michael Faraday spoke about a classic source of light: a hot material (here, the flame of a candle) emitting light, known as thermal light. We find this process in a light bulb as well as in the radiation produced by the sun and stars or in the Olympic torch. In nature, other sources of light are rather rare, such as lightning, auroras, or the bioluminescence of a firefly. On the other hand, technology has made different (non-thermal) light sources available, e.g., fluorescent lamps, lasers, and light emitting diodes.
Almost without exception, all light sources share a basic process in which electrons (or a system of electrons) return to a state of lower energy and release the energy by emitting photons. Beforehand, the electrons have to be brought into a state of higher energy. It is possible for this so-called pumping mechanism to occur in a number of ways: through the absorption of photons, through collisions of high-velocity particles in a very hot environment, or in semiconductors via electrical current. The light emitted by each source has a characteristic spectrum.
3.1 Thermal Light
Unaided, we can detect that a hotplate on a stove is overly heated in two ways: one via the red glow perceived by our eyes and also via the thermal radiation that receptors in our skin perceive as warmth. In both perceptions, electromagnetic radiation emitted by the hotplate in relation to its temperature is involved. Only a small part of the energy lies in the visible portion of the spectrum and is perceived by the eye (Table 3.1). While our eyes react to only a limited part of the spectrum, our sensory system for heat reacts to all the absorbed radiation energy, independent of the wavelength. If the hotplate cools down, the total radiated energy diminishes and the visible portion is reduced even more rapidly (Table 3.1).
Table 3.1
Electromagnetic radiation emitted spontaneously from a hot material as a function of temperature. The radiant emittance describes the emitted power per area. With decreasing temperature, the visible part of the radiation decreases very rapidly. (The figures are upper limits, not reached by all materials)
Temperature | Emittance kW/m2 | Power fraction in visible part (0.4–0.7 μm) | ||
|---|---|---|---|---|
°C | °F | |||
5,600 | 10,112 | 70,000 | 0.3 | Sun |
700 | 1,292 | 50 | 10−6 | Glowing hotplate |
400 | 752 | 12 | 3 × 10−10 | Hot hotplate |
100 | 212 | 1 | 3 × 10−20 | Teapot |
0 | 32 | 0.3 | 10−28 | Iceberg |
The surface of the sun, the hotplate, human skin, and an iceberg, thus, all have in common that they spontaneously radiate electromagnetic waves in accordance with their temperature. Even an iceberg at night radiates an ample amount of energy per square meter. The origin of this radiation lies in the thermal movements of the molecules in every material that only cease at a temperature of absolute zero. Between thermal radiation and light, there is no fundamental difference except the wavelength.
Light that is radiated spontaneously from a hot material is termed thermal light. This describes the light in the visible part of the spectrum. Stars, glowing iron, and the tungsten wire of a light bulb give off thermal light. The radiation of these emitters is never limited to the visible range but, depending on the temperature, also contains ultraviolet and infrared portions. Figure 3.1 shows the spectra for several temperatures. Some simple laws are applicable: (a) with increasing temperature, the power per radiating area increases rapidly2; (b) the wavelength of the spectral maximum is inversely proportional to the absolute temperature, meaning that the lower the temperature is, the further the radiation will be in the infrared, i.e. further away from the visible range. For the radiation of a body at room temperature, the spectral wavelength maximum lies at roughly 10 μm.


Fig. 3.1
Thermal radiation (power per radiating area) in the ideal case (the possible maxima). For the sun’s surface temperature (5,860 K), the maximum lies in the visible range; for a human’s surface temperature, it lies far in the infrared. The visible spectrum (between 0.4 and 0.7 μm) is indicated
A naked human body radiates several hundred watts, although almost totally in the infrared (maximum at ca. 10 μm). In an environment that is at the same temperature as our bodies, we receive approximately the same amount of radiation that we give off. In a cold environment, this balance no longer holds and we tend to freeze. By the way, the evaporation of perspired water (sweating) also takes away heat just as a cool blast of wind does.
The curves in Fig. 3.1 are derived from Planck’s equation, which exactly specifies the behavior of the thermal light spectrum for any given temperature. Planck3 developed it in 1900 based on purely theoretical considerations. Strictly speaking, the curves represent the spectral intensity that cannot be exceeded by any emitter. However, it is an empirical fact that many radiating bodies operate very close to this limit, such as the sun or the filaments of incandescent light bulbs (Fig. 3.2).


Fig. 3.2
Max Planck
Well-known applications of these laws are the heat distribution images of buildings or of somatic regions (Fig. 3.3). The intensities of the recorded radiation as a measure of the temperature of the radiating object are displayed in pseudo-colors. This measurement principle is unproblematic if it is known that the radiation of the body or object involved obeys Planck’s curves. In materials such as a wall, earth, water, or human skin, this condition is nearly but not precisely fulfilled. Better precision can be obtained with instruments that determine the temperature from the radiation ratios of two different wavelengths.
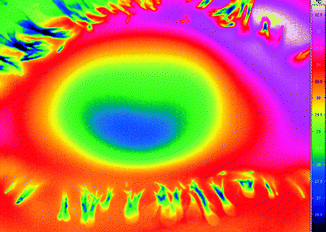

Fig. 3.3
Thermal image of an eye. The camera determines the temperatures from the infrared radiation and displays them in pseudo-colors
3.1.1 Luminous Efficiency
The thermal generation of light, e.g., with incandescent light bulbs, has low optical efficiency because only a small portion of the emitted radiation lies in the visible range. This is determined by the fraction of the light that the eye’s daylight spectral sensitivity curve V λ selects from the spectrum produced by the light radiator. Figure 3.4 shows the efficiency as a function of temperature T. For T = 2,800 K, it amounts to only 2.5 %; the rest is heat. Even at solar temperatures, where the overlap between the Planck spectrum and the V λ curve is almost optimal, the efficiency reaches only 14 % (Fig. 3.5). Therefore, it is understandable that fluorescent tubes or light emitting diodes, which give off their energy almost completely in the visible range, rate much better with regard to efficiency than do thermal light radiators (Table 3.2).
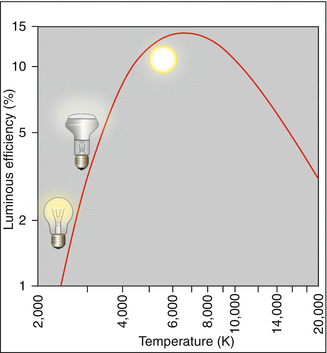
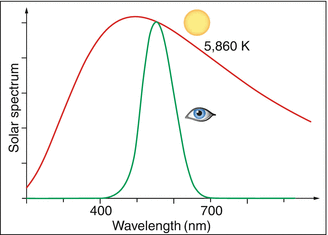

Fig. 3.4
Efficiency of thermal light as a function of the emitter’s temperature. Ordinate: luminous efficiency in percent. The luminous efficiency is the part of the radiant energy utilized by the eye

Fig. 3.5
Our eyes utilize 14 % of solar radiation. Red: spectrum of the solar radiation (5,860 K). Green curve: utilized by the eye
Table 3.2
Conversion of electrical energy into light: comparison of various light sources. The luminous efficiency is the part of the applied electrical energy converted into light and utilized by the eye. It is presented in percentages of the best possible conversion. This is given by light of 560 nm, generated with the complete conversion of the electrical energy into light energy
Light source | Luminous efficiency (%) |
|---|---|
Light, wavelength 560 nm | 100 |
Sun (5,860 K) | 14 |
Light bulbs, halogen lamps | 2–3 |
Fluorescent tubes | 7–10 |
Commercial white LED | 5–12 |
Sodium vapor lamp | 30 |
3.2 Fluorescent Tubes
The basic principle of fluorescent lighting is very simple: an electrical voltage between two electrodes causes a gas to glow. More precisely, it is free electrons that are accelerated between the two electrodes and collide with the gas atoms. The principle was discovered in 1858 (Geissler tubes). In the 1880s, fluorescent light bulbs were already being produced in large numbers, although mainly for entertainment purposes. Fluorescent bulbs in the form of the traditional straight tubes (Fig. 3.6) and as energy-saving bulbs have yields that are three to six times those of “normal” incandescent light bulbs. In typical constructions, mercury atoms are the sources of the radiation. However, this radiation lies in the ultraviolet range and is transformed into visible light by the fluorescing interior coating of the glass tube. By means of the coating, various spectra can be generated: cold, warm, and colored. In contrast to thermal sources, fluorescent tubes do not have a continuous spectrum but one consisting of discrete lines.


Fig. 3.6
Fluorescent bulb with a fluorescing layer on the inside of the glass tube, the prototype for modern energy-saving bulbs. When turned on, the starter (S) generates a high-voltage pulse
Sodium vapor, low-pressure bulbs function similarly but need no fluorescing wavelength conversion because sodium, unlike mercury, has visible emission lines. The light is engendered directly in the yellow-orange sodium double lines (589 nm). The light yield can be up to twice that of a fluorescent tube. We encounter these lamps mainly in the form of street lamps.
3.3 Light Emitting Diodes (LEDs)
The light emitting diode is the child of the semiconductor technology of the previous century. Among the semiconducting materials are silicon or germanium crystals. As the name indicates, they can conduct electrical current, but only poorly. In their ability to conduct electricity, they stand between isolators (glass, for example) and conductors (metals). In technological applications, traces of other elements are intentionally added to semiconductors; i.e., they are “doped,” which improves their ability to conduct electricity and makes it less temperature-dependent. Semiconductors were first used in rectifiers, which permit electrical current to pass preferentially in one direction, an effect that was explained for the first time by Schottky in 1939.4 Today, this type of rectifier consists of two semiconductor layers that are doped differently. The next application was the transistor, consisting of three semiconductor layers that allow a weak electrical current to steer a far stronger one. The transistor has massively transformed the technology of the past few decades, primarily as the basic element of highly complex circuits in computer microprocessors.
< div class='tao-gold-member'>
Only gold members can continue reading. Log In or Register to continue
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


