Keratometry
Michael K. Smolek
Stephen D. Klyce
Keratometry is the optical process of determining the curvature of the central cornea. Typically, keratometry is expressed as dioptric power (D) or as dioptric curvature (Kd) of the cornea. Dioptric power measurements are useful for assessing the cornea’s contribution to the overall refractive state of the eye and for the detection of corneal distortions that may be indicative of various diseases and disorders. On the other hand, keratometry can also be expressed as the radius of curvature of the cornea (the inverse of corneal curvature), which is mostly relevant for fitting contact lenses. Whereas curvature is normally expressed in inverse meters (m−1), in accordance with the manner in which optical vergence is expressed, the radius of curvature is normally expressed in millimeters, which is a far more practical measurement for the base curves of contact lenses. Keratometry is one of the simplest and most informative clinical measurements than can be made of the eye, and so it will remain an important and relevant diagnostic tool to assess a patient’s visual potential.
HISTORICAL BACKGROUND
Corneal curvature has been of interest to vision scientists for centuries. A description of corneal curvature was first reported in 1619 by Christoph Scheiner. He compared the apparent size of images of window panes viewed by reflection from the cornea with the relative size of the images seen in glass marbles of various size held next to the eye. By trial and error, Scheiner could find the ball that produced a similar-sized image to that seen in the cornea, and which was therefore equivalent in curvature. The first device built exclusively for keratometric measurements was constructed in 1796 by Jesse Ramsden, who used the device to study the possibility of corneal accommodation in aphakia (1). This instrument did not promote significant scientific interest until 1854, when Herman von Helmholtz improved on Ramsden’s keratometer design to facilitate his work in the rapidly growing science of physiologic optics (2). Essentially the device was built around a low-power telescope that could magnify and permit measurement of the first surface corneal reflection located immediately behind the cornea. The image is the reflection of a bright object (i.e., mire) of known size and distance. The ratio of the apparent size of the reflected mire image to the size of the actual mire allows corneal curvature to be determined precisely.
Helmholtz referred to his process of measuring corneal curvature as ophthalmometry and the device as an ophthalmometer. This terminology is still used today, but as Emsley pointed out, it is confusing because it implies measurement of the whole eye and not just the cornea (3). For this reason, keratometry and keratometer are the more commonly used terms today, although some manufacturers still use the term ophthalmometer. Although Helmholtz devised a successful experimental device, the first practical keratometer that was suited for clinical use was developed by Javal and Schiötz in 1881 (4). Many improvements have been made to keep the keratometer current with modern ophthalmic standards, but the basic optical design of these instruments has changed very little over the last century. In 1932, the Bausch & Lomb company introduced improved focusing, circular mires for better qualitative assessment of astigmatism, and simultaneous curvature measurement along orthogonal meridians, which significantly improved the ease of use of the keratometer.
DETERMINATION OF THE RADIUS OF CURVATURE
Strictly speaking, neither corneal curvature nor the radius of curvature are measured directly by a keratometer, but these values are calculated from the apparent size of the image of a bright object (the mire) viewed by reflection from the anterior corneal surface (actually from the tear film), which acts as a convex mirror. The formula for a convex mirror states that
the radius of curvature, r, of a spherical mirror is proportional to the ratio of image to object size:
The ray trace diagram of Fig. 8-1 shows that the image h’ is formed behind the curved mirror surface as a minified, virtual, erect image of the mire object of height h. Because the
distance, x, from the mire to the principal focus of the convex mirror is never known precisely, the distance, d, from the mire to the convex surface (i.e., to the corneal apex, A) is used instead. As long as d is relatively large, the calculation is sufficiently accurate to allow a small error in working distance. When the formula is applied to the cornea, the radius of curvature is always expressed as a positive number in millimeters.
distance, x, from the mire to the principal focus of the convex mirror is never known precisely, the distance, d, from the mire to the convex surface (i.e., to the corneal apex, A) is used instead. As long as d is relatively large, the calculation is sufficiently accurate to allow a small error in working distance. When the formula is applied to the cornea, the radius of curvature is always expressed as a positive number in millimeters.
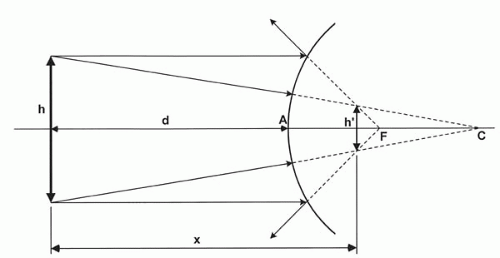 FIG. 8-1. Optical ray-trace construction of the virtual image of an object as seen by reflection from a convex mirror. |
The size and distance of the mire from the cornea places the mire image typically within the central 3 to 4 mm of the cornea. This location encompasses the region of the normal cornea that tends to be most spherical. The location is also within the region of the cornea in front of the entrance pupil that is most useful for vision under normal daytime lighting (the average photopic entrance pupil is approximately 4 mm in diameter).
One of the difficulties that must be overcome when measuring the size of the virtual mire image is that eye movements make direct measurements relative to an eyepiece reticule scale impossible to perform with any degree of accuracy. Ramsden was an astronomer who understood that the doubling prism micrometers that were used with telescopes to measure the size of celestial objects like the sun could be adapted to measure mire images in the presence of normal eye movements. Essentially, a doubling prism allows the operator to see two images of the same mire image displaced with respect to one another. When the side of one image is aligned to just touch the side of the fellow image, the overall size of the image can be determined even when the image is constantly moving. The doubling prism method is still used in modern keratometers, although the mire targets are more refined and have fiducial marks to make alignment even easier.
DETERMINATION OF CORNEAL POWER
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


