Fig. 27.1
ΔITD thresholds for four listeners are shown by symbols. Data for L2, L3, and L4 are offset vertically by 20, 50, and 60 μs, respectively. Error bars are two standard deviations in overall length. The dotted line is the maximum-likelihood fit to a 1/f law. The dashed line is the maximum-likelihood fit to the form 1/ (f c − f) η
It is possible to fit the dramatic lateralization failure at 1,450 Hz with a signal processing theory that extends the Jeffress (1948) model of the binaural system. The theory has two main parts. One part is an array of coincidence cells in the midbrain operating as cross-correlators, as observed physiologically in the medial superior olive (MSO) (e.g., Goldberg and Brown 1969; Yin and Chan 1990; Coffee et al. 2006). The second part is a hypothetical binaural display that is a nexus between the coincidence cells and a spatial representation that is adequate to determine laterality for a listener. The display is imagined to have a wide distribution of best delays with only a weak frequency dependence.
2.3 Centroid Theory
The centroid lateralization display was introduced by Stern and Colburn (1978) and applied to the lateralization of 500-Hz tones with interaural time and level differences. It was modified and extended to other frequencies by Stern and Shear (1996) to fit the lateralization data of Schiano et al. (1986). In this model display, a sine tone with angular frequency ω and an ITD of Δt excites midbrain cross-correlators represented by a cross-correlation function c(ωτ), where τ is the lag and values of τ have a density distribution p(τ|ω), centered on τ = 0.
The operative measure of laterality is the centroid of the density-weighted cross-correlation,
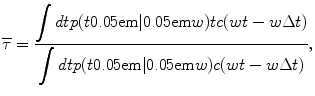
and the integrals are over the range of minus to plus infinity.
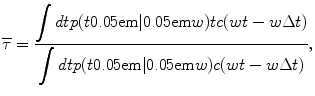
(27.1)
Values of 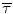 can be computed given reasonable choices for c(ωτ) and p(τ|ω). A reasonable choice for c(ωτ) is a cosine function, at least for frequencies of 750 Hz and higher,
can be computed given reasonable choices for c(ωτ) and p(τ|ω). A reasonable choice for c(ωτ) is a cosine function, at least for frequencies of 750 Hz and higher,

Parameter m (m ≤ 1) is the “rate-ITD modulation.” The density of lag values can be modelled as a constant for very small τ followed by an exponentially decaying function of τ, independent of frequency as per Colburn (1977).
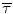 can be computed given reasonable choices for c(ωτ) and p(τ|ω). A reasonable choice for c(ωτ) is a cosine function, at least for frequencies of 750 Hz and higher,
can be computed given reasonable choices for c(ωτ) and p(τ|ω). A reasonable choice for c(ωτ) is a cosine function, at least for frequencies of 750 Hz and higher,
(27.2)
As pointed out by Stern and Shear, if the width of p(τ) is chosen correctly, then as the tone frequency increases, more and more cycles of c(ωτ − ωΔt) fit within the range of lags given by p(τ). This has the effect of preventing the centroid from increasing much as Δt increases because of partial cancellation of the positive lobes of c(ωτ − ωΔt) by the negative lobes. Because the centroid is the cue to laterality available to the listener, limiting the centroid in this way limits the perceived laterality. That limit could be a key to the failure to lateralize at 1,450 Hz and above.
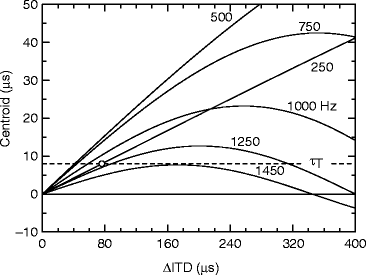
Values of centroid 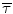 computed from the model are shown in Fig. 27.2 for m = 0.4 and for six different tone frequencies. Predictions for a threshold ΔITD can be made if it is assumed that there is a threshold value of centroid
computed from the model are shown in Fig. 27.2 for m = 0.4 and for six different tone frequencies. Predictions for a threshold ΔITD can be made if it is assumed that there is a threshold value of centroid 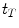 . For example, if it is assumed that the centroid threshold is
. For example, if it is assumed that the centroid threshold is 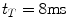 , as shown by the dashed horizontal line in Fig. 27.2, then the model predicts that the threshold disappears altogether as the frequency approaches 1,450 Hz. However, in order to model the faster than exponential increase in threshold, the rate modulation m must decrease rapidly with increasing frequency.
, as shown by the dashed horizontal line in Fig. 27.2, then the model predicts that the threshold disappears altogether as the frequency approaches 1,450 Hz. However, in order to model the faster than exponential increase in threshold, the rate modulation m must decrease rapidly with increasing frequency.
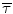 computed from the model are shown in Fig. 27.2 for m = 0.4 and for six different tone frequencies. Predictions for a threshold ΔITD can be made if it is assumed that there is a threshold value of centroid
computed from the model are shown in Fig. 27.2 for m = 0.4 and for six different tone frequencies. Predictions for a threshold ΔITD can be made if it is assumed that there is a threshold value of centroid 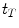 . For example, if it is assumed that the centroid threshold is
. For example, if it is assumed that the centroid threshold is 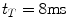 , as shown by the dashed horizontal line in Fig. 27.2, then the model predicts that the threshold disappears altogether as the frequency approaches 1,450 Hz. However, in order to model the faster than exponential increase in threshold, the rate modulation m must decrease rapidly with increasing frequency.
, as shown by the dashed horizontal line in Fig. 27.2, then the model predicts that the threshold disappears altogether as the frequency approaches 1,450 Hz. However, in order to model the faster than exponential increase in threshold, the rate modulation m must decrease rapidly with increasing frequency.
Fig. 27.2
Interaural delay centroid as computed in the centroid display model for six tone frequencies. An illustrative value of centroid threshold τ T is shown at 8 ms. It predicts, for example, that for a 250-Hz tone, the ΔITD threshold is 76 μs, and that for 1,450 Hz, there is no threshold at all
3 Low Frequencies
All models for the neurophysiological processing of ITD depend on the cross-correlation between the neural inputs from the left and right ears. The cross-correlation function provides a measure of the difference the phase or timing of signals arriving at the two ears and thereby encodes the azimuth of a source. But although there is a general agreement about the importance of cross-correlation, there are differences of opinion about how it is applied functionally. The 1948 Jeffress model imagines a doubly tuned array of cross-correlators, tuned in best interaural delay and tuned in frequency. The tuning in best delay is normally thought to be influenced by the largest possible delay in free field given the head size, but is otherwise rather broad, enabling a place model for localization. Tones with different ITD cause different neurons in the central auditory system to light up.
An alternative model abandons the concept of place process. Physiological studies of single units in the inferior colliculus of guinea pigs show a strong correlation between the best interaural delay Δt and the best frequency f. The relationship is such that the phase angle fΔt is in the neighborhood of an interaural phase of 45° (McAlpine et al. 2001). The two different models correspond to different mathematical forms for the density p(τ).
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


