Fig. 5.1
Schematic of the stimuli used in the TMC, FDMC and AFM methods, panels a, b and c, respectively. Double-headed arrows indicate the stimulus that was adaptively varied. M masker, S signal
For the AFM method (as described in Plack and O’Hanlon 2003), the signal was a 6-ms, 4-kHz sinusoid and the forward maskers, M1 and M2, were samples of white noise strictly bandlimited between 3,500 and 4,500 Hz. The duration of M1 was either short (10 ms) or long (200 ms). The duration of M2 was always 10 ms. The maskers and signal (when present) were temporally nonoverlapping as shown in Fig. 5.1c. The AFM method had two phases. Phase 1 measured masker levels at threshold for which M1 and M2 were equally effective in masking a 10- or 30-dB SL signal. Phase 2 measured signal level at threshold in the presence of either M1 alone, M2 alone or M1 and M2 combined (M1 + M2), where maskers were fixed at the levels obtained in phase 1 to mask a 10- or 30-dB SL signal.
2.2 Results
The mean TMC and FDMC results are presented in Fig. 5.2 (left and right panels, respectively). Linear regression provided good fits (average R 2 = 0.995) to both the mean off-frequency TMC and FDMC data, with slopes of 0.32 and 2.13 dB/ms, respectively. The overall shape of both on- and off-frequency TMCs is similar to that reported previously (e.g. Plack and Drga 2003; Lopez-Poveda et al. 2003), and the overall shape of the FDMC function is similar to TMC functions reported here and in earlier studies.
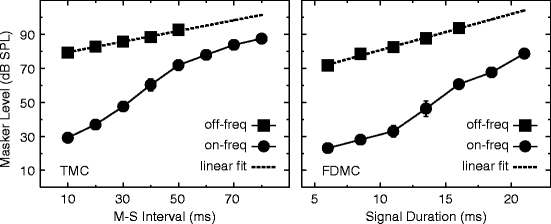

Fig. 5.2
Mean TMC (left panel) and FDMC (right panel) results, showing the masker level at threshold as a function of masker-signal silent interval (TMC) or signal duration (FDMC) for an on-frequency (circles) and an off-frequency masker (squares). Linear fits to the off-frequency mean data are shown by the overlaid dashed line. Standard error bars are also shown
The mean AFM results from phases 1 and 2 of the AFM experiment are presented in Fig. 5.3. The left panel presents data from phase 1, and the middle and right panels present mean data from phase 2 with a short or long M1 masker, respectively. Thresholds obtained for the M1 + M2 masker are greater than thresholds for short M1, long M1 or M2 masker alone, and excess masking (>3 dB difference) is observed at the higher level.
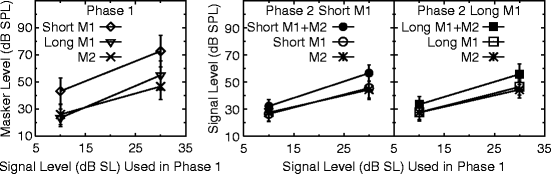

Fig. 5.3
Mean results of the AFM experiment. Left panel shows the results of phase 1. Middle and right panels show the results of phase 2. Phase 1 and 2 masker-signal levels at threshold are shown for a 10- or 30-dB SL signal
Mean response functions were obtained from the AFM data for each listener by applying the fitting procedure described by Plack and Arifianto (2010). Inferred BM response (input–output (I/O)) functions for the TMC and FDMC data were derived by plotting off-frequency vs. on-frequency masker levels, paired by masker-signal silent interval (TMC) or by signal duration (FDMC). The derived I/O functions are shown in Fig. 5.4 (left panel). The TMC and FDMC data points are connected by faint dashed lines representing the 3rd-order polynomial fit to the I/O functions. The response functions show typical non-linear I/O characteristics; i.e. a steep portion (for low input levels) followed by a shallow portion (input levels around 40–60 dB SPL). Compression exponents were obtained by differentiating the 3rd-order polynomial fits to the I/O functions and are shown in Fig. 5.4 (right panel). Two measures of compression were obtained: an average value of compression exponent for inputs between 40 and 60 dB SPL (CE40–60) and a minimum value (CEMin). The maximum level of gain (GainMax) was estimated as the difference between off- and on-frequency maskers for the smallest masker-signal silent interval of 10 ms (TMC) or the shortest signal duration (FDMC).
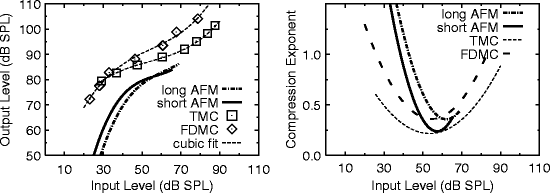

Fig. 5.4
Mean derived I/O functions (left panel) and compression exponents (right panel) for TMC and FDMC methods (open squares and diamonds, respectively), overlaid by a 3rd-order polynomial fit to the data shown by a dashed line. Also shown are mean derived I/O functions and compression exponents for AFM with a long masker (dashed-plus-dotted line) and AFM with short masker (solid bold line). Note that the vertical locations of the AFM I/O functions are arbitrary
Prior to the analysis, data outliers were eliminated by use of Tukey’s method, which defines outliers as greater than 1.5 interquartile ranges below the 25th percentile or above the 75th percentile (Tukey 1977). One-way ANOVAs with main factor of method (4 levels) did not show a significant effect for values of either CE40–60 or CEMin, but revealed a significant effect for the input masker level associated with CEMin, F (3,15) = 3.30, p < 0.05, with effect size, η 2 = 0.40. Post hoc paired t-tests (Bonferroni corrected) revealed that the FDMC method resulted in CEMin at lower input masker levels than the TMC method [mean difference between input masker levels = 3.40, SD = 1.86, t(5) = 4.61, p(two-tailed) < 0.01]. Estimates of GainMax from TMC and FDMC methods did not differ significantly. Pearson’s r revealed a significant negative correlation between absolute threshold and values of GainMax estimated from TMC [r(5) = −0.82, p(one-tailed) < 0.05] and FDMC [r(5) = −0.74, p(one-tailed) < 0.05] methods. Absolute thresholds were also found to be highly correlated with input levels associated with CEMin for TMC [r(5) = 0.93, p(two-tailed) < 0.05], FDMC [r(5) = 0.97, p(two-tailed) < 0.01] and long AFM [r(5) = 0.87, p(two-tailed) < 0.05].
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


