, Maneli Mozaffarieh1 and Hans Bebie2
(1)
Department of Ophthalmology, University of Basel, Basel, Switzerland
(2)
Institute for Theoretical Physics, University of Bern, Bern, Switzerland
Abstract
Ray optics (or geometrical optics) describes light propagation in terms of rectilinear paths in homogeneous media. The simple concepts of ray optics are very powerful in explaining image formation by mirrors, lenses, and the eye and in a multitude of optical instruments. The design of photographic objectives, which may consist of a dozen lenses to optimize image quality, is done within the framework of ray optics. However, we know that ray optics does not account for all phenomena in the propagation of light. Diffraction and interference cannot be understood without taking into account the wave nature of light.
19.1 Ray Optics or Wave Optics?
Ray optics (or geometrical optics) describes light propagation in terms of rectilinear paths in homogeneous media. The simple concepts of ray optics are very powerful in explaining image formation by mirrors, lenses, and the eye and in a multitude of optical instruments. The design of photographic objectives, which may consist of a dozen lenses to optimize image quality, is done within the framework of ray optics. However, we know that ray optics does not account for all phenomena in the propagation of light. Diffraction and interference cannot be understood without taking into account the wave nature of light.
How are these two models, light as rays and light as waves, related? Physics offers a very simple basic explanation: first, as long as the quantum theory is of secondary importance, all optical phenomena can be completely explained by the electromagnetic wave nature of light (Maxwell’s theory). Second, the concept of light rays represents a surprisingly good approximation to the wave theory. As usual, approximations are simpler to handle, but they have their limitations. In this chapter, we illustrate the relationship between the two models in terms of the image formation of a source infinitely far away by a collecting lens (Fig. 19.1).
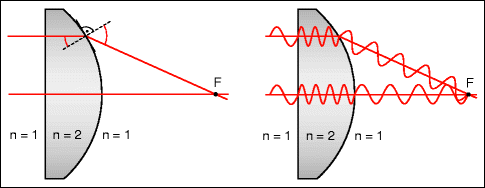

Fig. 19.1
Ray optic and wave optic explanations of the focus for parallel rays passing through an ideal collecting lens. Left: According to ray optics, the focusing results from the law of refraction when the rays leave the lens. Right: According to wave optics, the focus is that place where all contributions arrive with the same phase and thereby interfere constructively (the same number of periods along all the paths). Lens with a refractive index n = 2, in vacuum
It terms of ray optics, the position of the focal point F is determined by the law of refraction as the ray leaves the curved back surface of a lens (Fig. 19.1, left). The focal length, thus, follows from the refractive index of the lens and from the curvature of its surfaces. Nevertheless, focusing can also be explained using wave optics: the focal point is exactly the location where the light waves – as they travel down all the ray paths – have experienced exactly the same number of periods. In other words, all contributions arrive at the focal point in phase and produce constructive interference (Fig. 19.1, right): off axis, the light travels a shorter distance across the lens and, thus, for fewer periods than those that travel along the axis within the lens. This difference is exactly made up for by the longer distance from the point of exit from the lens to the focal point. For one point behind the lens – the focal point – this condition is fulfilled for all the rays. In locations that lie closer to or further away from the lens, the contributions from the various lens zones arrive out of phase and thereby almost completely cancel each other out.
While both diagrams are suitable for understanding how focusing occurs, the wave version offers a lot more additional information: if one shifts point F a little bit laterally away from the axis, the waves from the various lens zones still arrive almost in phase – the light intensity can, then, not be limited to the geometric point F. An analysis shows that only with a lateral offset on the order of λ ∙ f / (n∙D) or higher do the various contributions become substantially out of phase (λ: wavelength, f: focal length, D: diameter of the lens, n: refractive index of the medium between the lens and focus). This is the basis for understanding the Airy disk1: a parallel beam of light, passing through a lens, is not imaged as a point but, rather, as a small disk. Figure 19.2 shows the intensity profile. This blurring of the image cannot be avoided, even in the case of an ideally shaped lens.
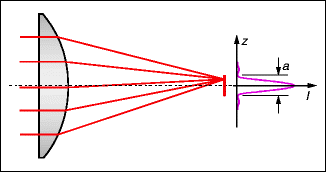

Fig. 19.2
Image of a parallel beam passing through an ideal lens in the focal plane, as explained with wave optics. Essentially, a disk (Airy disk) is illuminated in which constructive interference occurs. Outside the Airy disk, the various contributions cancel each other almost completely out. On the right, the intensity profile is indicated. The diameter between the zero locations is given by the equation a = 1.22λ ∙ f / (n∙D), where f is the focal length, D is the lens diameter, and n is the refractive index of the medium between the lens and the focal point. In typical lenses, the diameter of the Airy disk amounts to a few wavelengths
For the eye (n = 1.33, f = 23 mm, λ = 0.55 μm), the diameter a of the Airy disk for various pupil sizes D is listed in Table 19.1 – the smaller the pupil is, the larger the Airy disk will be. In addition to the wave optical limitations regarding the sharpness of the image that forms at the retina, imperfections also exist in the imaging media and interfaces. These increase with the pupil diameter. For a pupil size of 2 mm, in eyes with good visual acuity, both effects have roughly the same strength; in smaller pupils, the wave effect outweighs the other. However, for an ametropic eye, the view through an aperture of 1–2 mm in diameter can be beneficial – e.g., when trying to read a menu without glasses.
Table 19.1
Diameter of the airy disk in the eye for various pupil diameters
Pupil diameter D | 2 mm | 4 mm |
Airy disk diameter a | 12 μm | 6 μm |
a, in minutes of arc | ∼2′ | ∼1′ |
Intuitively, this phenomenon can also be understood as a consequence of diffraction at the pupillary edge. The smaller the pupil is, the larger the ratio of the pupil circumference to the pupil area will be since the circumference increases linearly while the area increases quadratically as a function of its diameter. Therefore, in very small pupils, the relative portion of the diffracted light increases and the image becomes more blurred.
19.2 Simple Lenses and Achromats
Often, the effects caused by the wave nature of light are of minor importance, so the approximation of ray optics can be applied. Examples include eyeglasses, optical instruments, and camera objective lenses. In principle, one follows the light rays on their pathways through the system, whereby the law of refraction determines the change in direction at each transition into a new medium. Camera objective lenses are optimized in this way even though a compromise between various residual errors must be accepted. Camera objective lenses owe their high degree of perfection to the large number of refractive surfaces, which permit a large amount of freedom in the optimization process. It should not be forgotten that the creation of objective lenses with practically no devastating residual stray light has been possible only with the invention of antireflective coatings.
A simple lens with spherical surfaces exhibits various aberrations. The most obvious one that occurs on the optical axis is spherical aberration (Fig. 19.3). Rays from the lens edges pass through the axis in closer proximity to the lens so that a parallel incident ray results in a spot at every image plane rather than a point. This error stems from the spherical shape of the lens surfaces. Non-spherical surfaces, which are more difficult to produce, are employed only for special purposes. They are also used for eyeglasses for greater degrees of ametropia. For a given focal length, the spherical aberration is less disturbing in lenses with smaller diameters. Conversely, this imaging error is at its largest with a ball-shaped lens. Nevertheless, fishes with ball-shaped lenses have sharp imaging because the refractive index gradually diminishes with increasing distance from the optical axis. The rays at the edges are less strongly deviated than in a lens with a homogeneous refractive index. In this way, sharp imaging is possible for every direction.


Fig. 19.3
Simple lens. Left: spherical aberration. With a larger f number (ratio of the focal length to the diameter of the lens), the spherical aberration is less important. For this reason, we see more sharply when there is good illumination (making our pupils smaller). Right: chromatic aberration. Due to the dependence of the refractive index on the wavelength, the focal length is smaller for shorter wavelengths
In human eyes, various factors help to attenuate the spherical aberration. The cornea becomes flatter toward the periphery. Its profile is more elliptical than spherical (Fig. 19.4). In addition, the index of refraction of the crystalline lens decreases toward the outside, but less than in fish eyes. The spherical aberration of the human eye for light that enters 2 mm off axis, which, if uncorrected, would have a value of 2 D, is thereby reduced by half. In addition, peripheral rays are perceived with lower sensitivity than axial ones are because of the angle at which the light reaches the photoreceptors (Stiles-Crawford effect).
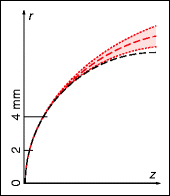





Fig. 19.4
Models of the anterior surface of the cornea. The deviation of the real elliptical profile (red) from a circle with the same radius of curvature in the center (black). Shaded area: Mean ± 1 standard deviation of the inter-individual variation of the (extrapolated) elliptical profile of the cornea. For a distance of 2 mm from the axis, the axial difference between the ellipse and the circle amounts to about 1 μm at a distance of 4 mm from the axis to 23 ± 15 μm (horizontal distances between the black and red lines). The spherical and elliptical profiles are extrapolated beyond the real pupil size. z and r tangential and axial coordinates
< div class='tao-gold-member'>
Only gold members can continue reading. Log In or Register to continue
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


