Fig. 2.1
Mean corneal radii of curvature and thicknesses
At the apex, a wide range of variation of the radius of curvature of 7–8.5 mm is compatible with good visual function, and in pathological conditions increases even more the spectrum. Short radii result in refractive power and high myopia. Conversely, large rays give a low dioptric power and farsightedness. Furthermore, the central corneal curvature is often not equal in all meridians. The focus of the rays reflected by a point object does not form a point image on the retina. In these cases occurs astigmatism (a, without; stigma, point).
The curvature of the cornea changes somewhat with age. It is more spherical in childhood and changes to the rule astigmatism (more curved horizontal meridian) in adolescence.
Then again it becomes more spherical in adulthood to turn against the rule astigmatism (steepest vertical meridian) with senility.
The thickness also varies from the center to the periphery. This causes the difference in curvatures of the anterior and posterior surfaces. It has an average value of 0.5 mm center, increasing toward the periphery at an average of 1.2 mm at the limbus (limit of the cornea with sclera).
The corneal thickness is determined largely by corneal hydration that increases with increasing hydration and slightly with the age. The refractive index of the cornea is 1.376, and an average refractive power is 48.8 D (diopter). The concave posterior surface of the cornea is wetted by the aqueous humor, which has a lower refractive index (1.336), so that the average dioptric power in this area is −5.8 D.
To calculate the total dioptric power we rely on Gullstrand corneal thick lens equation, giving a value of 43 D, about 70 % of the overall refractive power of the eye. The lens only contributes 20 D convergence.
The cornea presents diurnal fluctuations in its topography in spite of relatively stable visual acuity. The factors involved in these variations are both physiological and anatomical, as the pressure of the eyelid, the time of day (especially during sleep), the tonicity of the tear film, and hormone levels.
2.2 Histology of the Cornea
To perform a structural study of the cornea it is necessary to know not only the geometry but profoundly its internal components and functions performed to maintain corneal integrity. Furthermore, due to cuts or laser ablations performed in refractive surgery, it is vital to understand the healing process of wounds and scarring and to predict the refractive outcome of such processes. In Fig. 2.2, there is a scanning electron micrograph of an incision with laser wavelength of 211 nm, where the Bowman is observed (top) and multiple layers of collagen fibers.


Fig. 2.2
Scanning electron microscopy of ablated cornea with a 211-nm laser (picosecond). Magnification 550x (Xin-Hua Hu, Ph.D., UC Irvine, CA, EEUU)
The cornea is composed of five layers:
1.
The epithelium consists of 5 or 6 layers of cells. The more superficial are flat and are superimposed like the skin, but are not keratinized. The following layers are arranged more stacked tightly together. Between epithelium and Bowman’s membrane there is a basal membrane of 60–65 nm thick.
2.
Epithelial cells form a layer of uniform thickness and great regularity. Their function is to maintain the stability of the tear film.
3.
Bowman’s membrane tissue is a transparent sheet of approximately 12 μm. It is acellular and is composed of densely packed collagen fibrils that are in random direction. Its absence in inferior animals is associated with a plasticity of corneal stroma.
4.
The stroma is composed of film layers that run the entire length of the cornea; although the bundles are interlaced with each other, they are nearly parallel to the surface. The sheets are bonded together only loosely and are formed by bundles of collagen fibrils (bands of 64 nm) separated by a basic substance and water mucopolysaccharides. The latter are responsible for maintaining the hydration and transparency of the cornea and sclera that is not clear and does not contain mucopolysaccharides. The content of cells per unit volume is small. The cell bodies are flat, so they are also arranged parallel to the corneal surface. This arrangement of optical fibers provides uniformity to the cornea. The stroma constitutes approximately 90 % of the thickness of the cornea.
5.
The Descemet membrane is approximately 10 nm thick. It is considered a secretion of endothelial cells. The membrane is comprised of type IV collagen fibers with similar characteristics to those of other basal membranes of blood vessels and lens capsule. It has a similar structure to the corneal stroma in terms of its regularity. It is highly elastic and represents a barrier against punctures.
The endothelium is a single layer of cells lining the Descemet membrane. Its inner surface is bathed by the aqueous humor. In humans the reproducibility of these cells is limited. The age causes cell loss and the remaining cells become larger and spread. Endothelial cells provide a barrier to the passage of water of the aqueous stroma. It prevents the cornea becoming hydrated with the aqueous humor. Cell losses are key factors the corneal edema and thickening of the thickness.
2.3 Corneal Wound Healing
The accidental or surgical injury of one or all of the layers of the cornea results in increased hydration and loss of transparency. Therefore, it is necessary and appropriate rapid healing of wounds to prevent scarring or opacities. The speed and the type of healing depend on several factors; among them are the anatomical location (limbal or corneal), the size of the wound, the layer of the cornea involved, bacterial, viral, or fungal infection, and drug administration therapeutic purposes. Thus, the damage of the corneal epithelium in general trauma heals in 24–48 h in a normal eye. Bacterial, viral, or fungal ulcers or those involving the deeper layers of the stroma can take weeks to heal. Therefore, deep laceration or surgical incision takes several weeks to heal completely.
The normal healing process of cuts on the central area of the cornea involves a cytological response and sleeve. Sometimes, for reasons not very clear, blood vessels can grow from the healed corneal tissue. The normal cornea is completely devoid of blood vessels. The capillaries extend just 1–2 mm beyond the limbal zone.
3 Measurements of the Mechanical Parameters
3.1 Extensibility of the Cornea
In 1937, Friedenwald [4] developed a formula which relates changes in intraocular pressure (IOP) with intraocular volume during Schiotz tonometry:
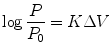
where P 0 = initial pressure; P = pressure following the change of volume ΔV; K = coefficient of ocular rigidity.
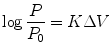
(2.1)
Friedenwald established that the value of K eyes remained constant for pressure higher than 5 mmHg (133 Pa/mmHg).
Many researchers, including Gloster and Perkins in 1957, attempted to determine experimentally the rigidity coefficient. Contradictory results were obtained concluding that K is not constant in the physiological range of IOP.
Therefore, the formula (Eq. 2.1) was invalidated. It was suggested that studies of the extensibility of the cornea and sclera in uniaxial test could help explain such changes. Already in 1864, Schelske gave way to a coefficient of elasticity for the cornea and sclera of humans and rabbits. He found that the coefficient for meridional scleral strips was 7 % more extensible than the equatorial, and the cornea was twice extensible than sclera. Weber in 1877 had found a large variation in scleral extensibility strips between different human eyes. Perkins and Gloster performed extensibility measurements with corneal and scleral strips isolated from rabbits, using weights that produce stresses as close as possible to those of a normal eye. They compared these results with the determinations made by the authors of the intact eye strain. They found that the eye became less distensible at high pressures, consistent with the fact that the scleral strips became less extensible to the increased tension to a certain point (20 N/m) where extensibility became more constant. But they also noted that the strips did not return to their original length after the weights were removed. They found the creep phenomenon (temporary slow deformation with time) in strips with an instant length change of 81.8 % and 6′ to reach the stationary state. During distension of the intact eye, the cornea and sclera extend in two directions where the stresses are distributed and the thickness decreases. In the case of uniaxial test strips there is a single direction, length, and decrease in both the thickness and width. Therefore, Perkins and Gloster did not justify performing a close analogy between distension of an intact eye and scleral and corneal strips.
Woo and Kobayashi [5] came to the same conclusion as Gloster and Perkins in human eyes. They added that exposing the free ends of collagen fibers caused a minor elastic response of the material and the straightening of the curved strips into a uniaxial test caused a significant error in elasticity measurements. They argued that it is important to consider, for volume changes to changes in IOP, the geometry variations and corneal material inhomogeneity. They did not consider the viscoelasticity and large deformations. Kobayashi and Woo devised a method for determining the elastic properties of the sclera and the cornea retaining its natural geometry. They sectioned equatorially enucleated eyes (1–3 days post mortem) and placed each half shell (anterior and posterior) in a pressure chamber. They found that both the shell and the subsequent previous corneosclera bear their weight without IOP. They measured with a scanner system the deformation of the horizontal surface while the pressure was increased. A photomultiplier detects the reflection of light at two targets located at two points of the cornea. The light was generated by a cathode ray tube driven by a triangular wave generator. They also measured lateral deformations (0°, 45°, 90°) to determine the isotropy of the material. They found that the deformation in three directions was very small. Moreover, they conducted a hysteresis test resulting in a minor viscoplastic (time dependent but not temporary deformation) effect. They considered the material as isotropic assuming that stresses across the thickness were only 10 % of the other planar strains in the corneal cap. Based on pressure–deformation curve measures, Woo and Kobayashi considered it also as nonlinear. In order to obtain stress–strain curves in the natural three-dimensional state of the cornea, they constructed a mathematical model [6] using effective stress and effective trilinear deformation.1 The model parameters were adjusted iteratively until deformations predicted by finite element analysis agreed with those obtained experimentally (a technique called inverse method). Once the fit is reached, trilinear relations were converted to an exponential function through least squares method (best fit optimization method), obtaining
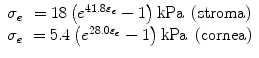
To validate the equation, a pressure–volume curve of the anterior segment of the eye was compared with experiments obtaining good agreement except for high pressure. Concentrated high stresses in clamped edges and possible swelling of the cornea by humid air are potentially the causes of high pressure discrepancy.
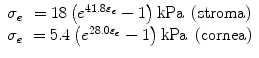
(2.2)
Schlegel et al. [7] investigated the viscoelastic properties in human enucleated eyes using ultrasonic waves by measuring changes in ocular diameter while IOP was cyclical. They found that pre-pressurized eyes had a substantially less viscoelastic response. Using the same protocol of Schlegel, Kobayashi et al. [8] determined the viscoelastic response of human corneas subjected to PIO from the same procedure of Woo et al. The purpose was to isolate the effect of viscoelastic pressure decay over time by measuring pressure with a tonometer. In pre-pressurized eyes the answer was almost negligible. The viscoelastic response was characterized in pre-pressurized eyes with a five-element linear viscoelastic model. They found average values of 53.68 ± 83.03′ to the slow time constant and 11.1 ± 0.71′ for the fast time constant. The average instantaneous elastic modulus was 1.11 MPa. A nonlinear viscoelastic mode l (Fung hereditary integral) found a better characterization of the viscoelastic parameters.
Greene and McMahon [9] studied in enucleated intact rabbit eyes the primary, secondary, and tertiary scleral creep function of temperature (26–48) and IOP (15–100 mmHg). In physiological conditions (37 °C and 15 mmHg), there is a speed creep of 0.06 %/h corresponding to 0.5 D/day. This measure has no physiological meaning in humans.
Russell and Klyce [10] modeled with FEM the corneal hydration regulation.
Parameters as permeability and solute transport through the intervening membrane were determined. It was simulated corneal hydration dynamics, thickness variations at different boundary conditions, such as hypertonic solutions, cold environments, high IOP (glaucoma), and destruction of limiting cell membranes (epithelium and endothelium). They predicted that the removal of the epithelium (as in laser photokeratectomy) causes an increase of the stromal thickness by 25 % for 1 h, consistent with the results in vivo.
Greene [11] examined the stresses undergone by posterior sclera at the accommodation produced by zonular fibers, convergence, vitreous pressure, and extraocular muscles. He noted that animals can myopize experimentally. He concluded that the oblique muscles are capable of originating local stress concentrations near the entry of the optic nerve.
Arciniegas et al. [12] found a relationship between the elastic modulus and the proportional limit with the age for high loads (σ >> 14 kPa) in 24 eyes of 24 human scleras of various ages. They found that from birth both are high and decrease with age to stabilize after 20 years approximately. This reflects that the surgery should be performed after stabilization refraction. While there may be other parameters to ensure this, it is possible that there is a dependent refractive corneal elasticity. Creep was also measured in corneal-scleral shells of 30 rabbits being of 1.4222 %/h for 20 mmHg a value higher than in rabbits (Greene and McMahon). One important measurement in the diagnosis of glaucoma was to compare the pressure measurements with the Goldmann tonometer and a sensor implanted within the vitreous chamber of the eye of a rabbit. They found an average of 2.74 times greater IOP measurement with the sensor. Deficiencies the Goldmann tonometer is allotted not consider in corneal thickness, mechanical properties, the geometric shape of the eye, and creep.
Nash et al. [13] conducted a uniaxial test strips for low loads (σ < 250 kPa), finding the nonlinear relationship, but found no association with age eyes because they took ages over 20 years. They determined that the elasticity in normal corneas and keratoconus were equal. Creep was measured in human strips with a load of 150 psi for 2–20 h, finding similar results compared in Greene and McMahon.
Kamm and Battaglioli [14] found that the compressive Young’s modulus through thickness is hundred times smaller than tensile (27–41 0.2 kPa). They also calculated Poisson’s ratio across the thickness (0.46–0.50) resulting in a nearly incompressible material in that direction. However, they explained that the hydration and viscoelastic effect could influence the results, being even a lower compressive modulus.
3.2 Keratoconus Biomechanics
Edmund [15], in 1989, conducted a study of 27 patients with keratoconus and 37 normal to determine and describe corneal topography and pachymetry of their eyes and to evaluate the hypothesis that the difference is elastic. Methods and descriptive models were developed for characterizing corneal shape based on the central curvature and radial variation coefficient, eccentricity and function of the central curvature, the corneal thickness profile, fitted with a parabola, and the corneal-limbal ring, adjusted to an ellipse. Also, methods for estimating Young’s modulus [16] and mass-based corneal topographic descriptive parameters were developed. An estimation of the stiffness from measurements of corneal tonometry with various weights and calibration tables from Friedenwald were derived.
He also showed that the stationary Young’s modulus and stiffness (which would be related to instantaneous Young’s modulus) is lower in keratoconus but have no correlation between them. It was shown that only in an advanced stage of keratoconus (>7.5 D) the corneal mass decreases. Based on the thickness and topographical changes, stress distribution is altered also based on the membranal theory (or law of Laplace) in keratoconic corneas. Tension along the meridian in normal corneas decreases while in keratoconic corneas increases. This increased tension would cause a second growth process of keratoconus in the corneal periphery as shown in the growth found in the periphery of the corneal thickness, contrary to the hypothesis of elastic keratoconus. It seems that the instantaneous Young’s modulus reflects the immediate response of the collagen fibers, to match the value calculated from the ocular rigidity in comparison with the experimental measurements cornea strips. While the Young’s modulus response appears to reflect steady elastic matrix glycosaminoglycans, consisting of the matrix compression and slippage of the collagen fibers, and that the estimated values are of the same order the Young’s modulus of the matrix, also indicating that the collagen fibers are rather relaxed in the physiological state. This would be consistent with the theory that the slippage increases keratoconus collagen fibers due to reduced adhesion to Bowman’s membrane and a matrix synthesis altered corresponding to an increase in the elasticity of the corneal tissue. Keratoconic biochemical studies demonstrating a normal collagen and altered proteoglycan synthesis confirm this hypothesis. On the influence of genetics and environment in keratoconus, see [Edmund] p. 30.
Hjortdal et al. [17] repeated the test of Woo and Kobayashi in ten corneas maintaining human corneal hydration normal IOP for a range of 2–10, 10–25, and 25–100 mmHg, finding values of 3, 9, and 20 MPa, respectively. The authors explain that the results of Woo and Kobayashi and Jue and Maurice give greater deformations due to greater corneal hydration. They assume that the values found still underestimate the Young’s modulus values in a constant corneal volume.
In 1996, Hjortdal [18] studied in vitro the elasticity of the cornea and limbus by regions. He found rigidity at the limbus preferentially in a circumferential direction and to a lesser extent in the peripheral cornea preferentially in a meridional orientation. The same study was made after four radial keratotomy incisions by Hjortdal et al. [19]. Normohydrated corneas were found to have an important role of local bending undamaged stromal tissue underneath the incision to generate the opening of the incision. He also found that compression of circumferential tissue disappears somewhere between the endothelium and epithelium to become taut.
Purslow et al. (1996) conducted a study of the relationship of IOP vs. volume based on the intrinsic stiffness Young’s modulus. They found a relationship between the incremental values of Young’s modulus at a given pressure proportion to the fourth power of the radius of the sphere eyepiece. They assumed that the Poisson’s ratio is 0.5 confirming experimentally pachymetric measures.
3.3 Stromal and Descemet Membrane Extensibilities
Jue and Maurice [20] studied the mechanical properties of the stroma and Descemet membrane separately, using the principles of measuring the geometry of the intact eye.
The system consisted of a keratometer that viewed through a reflection prism two drops of mercury placed in the corneal surface. Full enucleated eyes were taken from rabbits and humans aged 45–90 years. Hysteresis tests were performed, responses to low and high tension, of the cornea intact isolated stromal and membrane isolation. Descemet’s membrane is more extensible, in a nonlinear way. The stroma is virtually non-extensible and mimics intact corneal stromal mechanical properties.
From the high pressure curve, the elasticity modulus of the stroma is calculated. The stroma is composed of 70 % of its dry weight collagen fibers fi. The value of the elastic modulus of the collagen fibers can be obtained from the literature. Assuming constant voltage across the thickness, Laplace’s equation gives the value for the case of spherical surfaces of thickness t radius of curvature R, under an internal pressure IOP
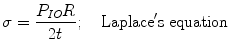
Dry stromal thickness is 0.07 mm; therefore, the thickness of collagen in the stroma is equal to 0.05 mm. Curve obtained high pressures relationship IOP/e which is 9.106 Pa. Then within 7 mm, the Young’s modulus (E σ/ε) of the stroma, without considering the extensibility of the ground substance, is in the order of 0.6 at 1 GPa. The procedure is to calculate the Young’s modulus of Descemet’s membrane at low tension. With a thickness of 12.5 μm, with a 150 cm H2O/unidad deformation, Laplace equation leads to 5 MPa.
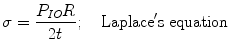
(2.4)
Considering the fundamental substance of stroma with a modulus of elasticity between 1 and 100 kPa (depending on stromal hydration) and as the volume ratio of collagen fibers and ground substance is 1:9 according to Maurice, we calculate the modulus of the stroma in fiber direction. This value has a range, depending on hydration of 11 MPa to 100 GPa.
Hanna et al. [21] used a mathematical technique to estimate the homogenization modulus of the stroma considering its fibrillar structure. This technique allows to describe macroscopic stress–strain relationship of materials whose microscopic structure is periodic. They conducted a model based on stromal microscopic measurements by X-ray diffraction of wet rat tendon similar (but not identical) to that of human corneal stroma and also based on transmission electron micrographs of human corneal stroma to estimate the relative contribution between the fibers and the ground substance. In the model we used the following values:
Collagen fibers 35 % by volume
Fiber diameter 25 nm
Space between fibers 48 nm
20 % hydration fixed (both for fibers and for substance)
E 1 GPa longitudinal fibers
Poisson’s ratios calculated for the fibers and the ground substance and the Young’s modulus for the basic substance, adjusting the coefficients until homogenization values, agreed with the experimental values found in the literature. The results are consistent with previous experiences, which validates the model clinically. For holographic interferometry, Kasprzak et al. [22] Elastic Modulus measured bovine corneal tangent for high pressures coincide with curves and Maurice Jue.
3.4 Bowman’s Membrane Importance
There are controversies regarding the role of Bowman’s membrane in corneal structure [23]. It is believed that Bowman’s membrane contributes to the stability of the corneal curvature and is also protective against injury and infections. While it has not been shown experimentally, this hypothesis is taken into account in refractive surgery to preserve it.
On the contrary, in photorefractive keratectomy, made with UV excimer laser or IR, the flattening is achieved by removing tissue from the anterior surface of the cornea, sacrificing central portions of Bowman’s membrane.
Clinical experiences indicate that Bowman’s membrane should be incised for changes in the anterior corneal curvature in refractive procedures.
Incisions within the stroma without breaking the Bowman’s membrane curvature will not change much anterior curvature, but it can change the posterior curvature. It is considered that the removal of part of the Bowman membrane Excimer laser is a potential source of instability in the cornea long term. Although such considerations have not been demonstrated clinically.
Theo Seiler et al. [24] conducted a study showing that after 6 months of an excimer laser photorefractive keratectomy, the refractive result was stable.
Hjortdal et al. [25] found no significant mechanical contribution of Bowman’s membrane in the instantaneous or short-term response.
3.5 Viscoelastic Parameters
Theo Seiler et al. [24] conducted a study of the viscoelastic properties of strips of cornea without Bowman’s membrane. Creep tests performed (tissue exposed to constant load, measuring the extent as a function of time) and stress relaxation (the tissue exposed to a constant elongation measuring the tension as a function of time) into strips enucleated eyes cornea. To remove the layer of Bowman, perform excimer laser keratectomy. The results showed that the strips of cornea are average stress–strain relationship with 5 % higher Bowman without it. This value could be higher because the experimental error was 10 %. Furthermore, viscoelastic properties in this experiment did not differ. They found a fast relaxation time of 10.58 and 269 s for the slow corneal stripping of Bowman’s membrane.
Smolek et al. [26] obtained spectrum by applying shear compliance spectroscopy technique compliance dynamic mechanical cutting cylindrical specimens explanted human corneas, according to corneal hydration and temperature, and in the frequency range of 0.1 MHz–100 Hz found that a myopic cornea is significantly softer than emetrópicas corneas in both low and high frequencies. They found that thickness change varies with the shear compliance significantly (600 times of 0.2–1 mm at 1 Hz) and also corneal hydration and temperature change significantly the shear compliance. They considered that it is important to detect the frequency range interest 0.1 Hz–1 MHz
Buzard et al. [27] monitored every 1 min corneal topography after placing a Honan balloon for 5 min, increasing IOP to 30 mmHg. Normal corneas found that very little change topography after 3 min in contrast corneas after 3 months of radial keratotomy flattened almost 1 D to 0.40 D minute to 3 minute. At 9 months this group flattened 0.10 D per minute. On jobs investigating corneal hydration and its implications for the CR, we refer the reader to the references [28–30, 10].
4 Biomechanical Models
In 1972, Woo et al. [5] input the results of the characterization of corneal and scleral field into a mathematical model by EF human corneal-scleral shell. This model was used to compute the nonlinear relationship between the intraocular pressure (IOP) and the volume of the eye and analyze the structural response during applanation tonometry [31]. The model was axisymmetric, with the geometry based on an idealized eye quadrilaterals with 665528 nodes. Bowman’s membrane had the same elastic properties with that of the stroma, Descemet’s membrane, and the sclera. Poisson’s ratio equal to 0.49 was considered. Tests were performed with Poisson’s ratio of 0.5 obtained differences in voltages 0.5 % to an IOP of 17 mmHg. The limbus was modeled by varying the elastic modulus in seven increments between stromal and scleral modules. They found that the tensions were greater at the limbus and at the Ecuador than in other areas. Other studies found that the stiffness coefficient decreased when Friedenwald increased IOP. The results were similar to data obtained in vivo by several researchers, but differed from results obtained in enucleated eyes because the model did not consider the additional stiffness post mortem produced in the choroid. In the simulation of applanation, modified stroma elastic properties (modulus perpendicular to the plane of the cornea = 20 kPa) to account for the collapsing of the collagen fibers under compression tonometer indenter. In this area the bending rigidity is decreased. They found that it is consistent with empirical results.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


