Most physiologic responses occur over ranges of amplitudes and in units of measure that are not familiar to the lay person. To fully appreciate the proper testing of CS, and to correctly interpret the resulting CSF, we need to define certain terms and concepts. Understandably, some of these terms are used synonymously and interchangeably in common language, but they have very specific definitions in the present context.

Luminance (L) is the physical amount of light emitted by a source or reflected from an illuminated object; the common unit of measure is candela per square meter, cd/m². Brightness is the perception of a luminous object by the human visual system, which can be affected by adaptation, aftereffects, and the presence or absence of other objects in the visual field.

Contrast (C) refers to the difference in luminance between an object (L_max) and its background (L_min), where the object is brighter than the background. The object itself may be small against the large, uniform background or, at the other extreme, it may be a single edge (not a repeating pattern) separating a light area from a dark area of visual space. Contrast is expressed as a ratio or percentage of this difference with respect to the object luminance,

C = (L_max – L_min) / L_max

Modulation (M) is the term for the contrast of a repeating pattern, commonly referred to as a grating, where it is not apparent which part of the pattern is the “object” and which is the “background.” An example is a series of light (L_max) and dark (L_min) stripes, as in the zebra in Figure 3.2. Modulation is calculated as the ratio of the difference of the luminances to the sum of the luminances,

M = (L_max – L_min) / (L_max + L_min),

where the luminance is measured across the spatial extent of each component part of the pattern. Alternately, modulation can be expressed by the mathematically equivalent ratio of the difference between maximal and average luminances to the average luminance (L_avg),

M = (L_max – L_avg) / L_avg,

where

L_avg = (L_max + L_min) / 2

The stripes in the image in Fig. 3.2B have the same average luminance as the stripes in Fig. 3.2A, but with decreased modulation. Note, if the dark part of the target is totally black (i.e., L_min = 0), then both contrast and modulation will be 100%, regardless of the nature of the target or pattern. On the other hand, a grating with light and dark areas of similar luminance will have a modulation very different from the contrast calculated for a single object
and background of the same respective luminances. For example, a grating with luminances of L_max = 55 cd/m² and L_min = 45 cd/m² has a modulation of 10%, whereas the comparable contrast of a single target and background with identical respective luminances is 18.1%. Most manufacturers of CS tests refer to their charts and instruments as presenting stimuli at certain “contrast” levels, but they correctly measure and report modulation values. In deference to this common usage, we will occasionally refer to targets as having high or low “contrast,” even when the precise term is “modulation;” the reader should understand from the context of the discussion which concept is actually being considered.

Threshold is the minimal stimulus level needed to induce a physiologic or cognitive response. The person, however, does not always need to be cognitively aware of the stimulus for a response to occur. For example, very few persons who are not presbyopic are conscious of retinal image blur as they accommodate for targets at different distances under normal circumstances. Sensitivity is the reciprocal of threshold. For the CSF, points plotted on the abscissa represent the least possible sensitivity, corresponding to targets of 100% contrast (or modulation).

The logarithm of a number represents that value as a power of 10. For example, typical human photopic vision extends from about 1 to about 65,000 cd/m². Mathematically, it is much easier to characterize this range as 0 to 4.8 log units. For the CSF, because of the potentially large ranges of responses for both spatial frequency and sensitivity, the data are commonly plotted on logarithmic scales on both axes, which results in the characteristic inverted-U shape of the function (see below).

Most spatial visual responses are properly specified by angular measures, such as degrees, minutes, or seconds of arc. Yet, the common expressions for eye movements and visual resolution are prism diopters and the Snellen fraction, respectively, both of which represent ratios of two linear distance measurements. Recall, one prism diopter is equivalent to a lateral displacement of one unit at a distance of 100 units, for example, a 1-cm shift at a 1-m distance. Likewise, the numerator of the Snellen fraction specifies the test distance, in feet or meters, and the denominator gives the reference distance at which the target subtends 5 arcmin; thus, we have the familiar designation of normal VA as 20/20 in English units and 6/6 in metric units.

The spatial frequency of a target indicates how many components of a repeating pattern, or grating, occur within a given area or space. For a series of stripes, one cycle represents one pair of light and dark stripes. The frequency is usually specified in cycles per degree (cpd). At a 20/20 acuity demand, each arm and gap of the letter “E” subtends 1 arcmin, with the entire letter subtending 5 arcmin. Thus, one cycle on the “E,” that is, one arm and one gap, subtends 2 arcmin. Because there are 60 arcmin in one degree, the “E” has a spatial frequency of 30 cpd. To convert between cpd and the comparable Snellen demand, observe that the product of the spatial frequency and the denominator of the Snellen
fraction is a constant: for 20-ft Snellen demand, use

600 = (spatial, frequency) × (Snellen, denominator),

and for 6-m Snellen demand, use

180 = (spatial, frequency) × (Snellen, denominator)

In Fig. 3.2, the zebra’s stripes are much narrower on the legs than on the neck. Therefore, the leg stripes have a higher spatial frequency. Also, in a complex presentation as in Fig. 3.2, different parts of the object may differ in phase and orientation. The stripes on the zebra’s legs are roughly horizontal and those on the torso are roughly vertical, demonstrating a difference in orientation. The stripes on the front and back legs, while having similar orientation and frequency, do not line up exactly, thereby demonstrating a difference in phase.

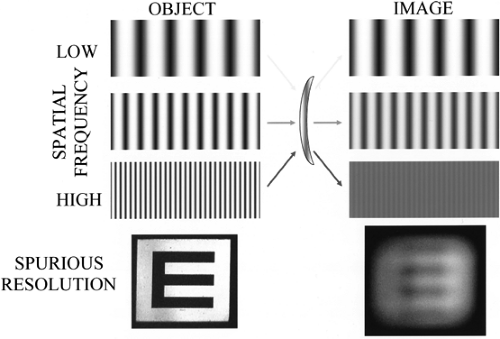
Modulation transfer is the ability of an optical system to produce accurately an image of an object, calculated as the ratio of the image modulation to the object modulation for a given spatial frequency. Because of diffraction, chromatic and monochromatic aberrations, and focus and power errors, the image will never be a perfect representation of the object. For low spatial frequencies, the image blur is hardly noticeable, whereas for high spatial frequencies, the image is almost fully obscured, as demonstrated in Fig. 3.3.

As an aberration or defocus increases, the resolving power of the system will be severely diminished, such that even middle (and, possibly, low) spatial frequency objects are imaged as a uniform gray. With sufficient defocus, however, the system may show spurious resolution, in which case the light and dark areas of the image exhibit a 180-degree phase shift (aka phase reversal) with respect to the object. Thus, for example, a person with uncorrected myopia of about 8 D might unexpectedly “see” a slightly blurry “E” at the top of a 20-ft letter chart; of course, that person will see the “E” with four arms rather than three!

Technically, a pattern of dark and light stripes is known as a square wave grating, where there is constant luminance across each stripe and a discrete change in luminance at the
border between stripes. A sine wave (aka sinusoidal) grating, on the other hand, offers a continuous change in luminance from maximal to minimal, and back to maximal again, based on the trigonometric sine function. The vertical stripes at the top of Fig. 3.3 are sine wave gratings, whereas the horizontal arms of the “E” at the bottom of the figure form a square wave grating.

Mathematically, a sine wave is a more pure function than a square wave: the sine wave comprises only a single spatial frequency. Much like the timbre of a musical instrument, or the combination of several different instruments playing the same note, a square wave has a fundamental frequency that corresponds to a sine wave having identical maximal and minimal locations and several harmonics or overtones that are merely multiples of the fundamental frequency. See Cornsweet (3), Schwartz (4), and Palmer (5) for a more in-depth analysis of this concept. Suffice it to say that the harmonic frequencies of a square wave are odd multiples of its fundamental frequency, and that the harmonic frequencies have greatly reduced amplitudes with respect to the fundamental frequency. A square wave grating that provides a nominal spatial frequency at 10 cpd, therefore, also provides (dimmer) spatial frequencies at 30, 50, 70, and so forth cpd. Consider that 10 cpd corresponds to a Snellen demand of 20/60, and 30 cpd corresponds to 20/20. Even if an individual has 20/20 VA, which requires measurement with a target of high contrast, that person would not be able to detect the low-contrast 30-cpd harmonic frequency, nor any other higher-order frequency. Thus, a 10-cpd square wave grating will appear to be identical to a 10-cpd sine wave grating.

For any manner of simple lenses (e.g., spectacles) or complex lens systems (e.g., telescopes and cameras), the modulation transfer function (MTF) gives the modulation transfer for all possible spatial frequencies. For the human visual system, the comparable set of responses is referred to as the CSF. Here, however, neural and cortical processing and the optics of the eye contribute to the final outcome. (The ensuing discussion presumes that we are not dealing with the extreme limiting cases of total blindness nor severely compromised neural or cortical functioning.)

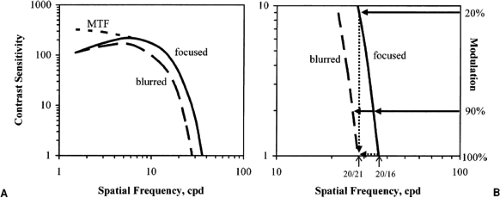
An idealized CSF is shown in Fig. 3.4 (solid line). Any target whose spatial frequency and
contrast (or modulation) plot on or below the curve will be visible to the observer; targets that plot above the curve will not be seen. The CSF may be thought to be composed of two distinct segments, namely, responses to high and low spatial frequencies. Note that “high” and “low” are relative terms, and that a consistent or discrete delineation is not seen between them. Responses to high spatial frequencies depend primarily on the quality of the preretinal optics (i.e., of the eye and any auxiliary lens or optical medium). Responses to low spatial frequencies are mediated somewhat by neural (i.e., retinal and precortical) processing (4). In addition, the CSF can be either enhanced or diminished via further processing in the cortex, as described in various conditions below.

The high-frequency endpoint, or cut-off, of the CSF corresponds to the patient’s VA, where target modulation must be at the maximum of 100% for the patient to report correctly seeing the target. In practice, most well-maintained charts and instruments used to assess VA provide targets with modulation of about 90%. As illustrated in Fig. 3.4B, this slight decrease in maximal modulation has little or no practical effect on the measured VA, even for a slightly defocused eye. Similarly, as suggested by Rabin and Wicks (6), a low degree of optical defocus (i.e., retinal image blur) will cause only a slight reduction in VA (about one line), but a significant reduction in CS, because of the steep slope of the CSF at the high spatial frequencies. In the condition illustrated in Fig. 3.4B, the same size target that can be distinguished at only 20% modulation with the focused eye requires 100% modulation to be seen with the blurred eye.

At the other end of the CSF, the low-frequency drop-off results from lateral inhibition at the retinal ganglion cells (3,4). This is the same phenomenon that produces Mach bands, the apparent increase and decrease in brightness on either side of an edge separating a light surface from a dark surface, respectively, although both surfaces have uniform spatial luminances. Figure 3.5 demonstrates this phenomenon; cover everything but any single square to confirm that no variation exists in luminance across that square.

With foveal viewing, the adult CSF typically reaches a peak at 3 to 5 cpd, although considerable variability exists in absolute sensitivity, even across normal adult observers (7,8). Some individuals may erroneously refer to the high sensitivity at the center of the CSF as a “middle-frequency enhancement,” suggesting that postretinal processing can exceed the modulation transfer limits of optical components governed at least by diffraction, not to mention spherical aberration, coma, chromatic aberration, and other higher-order aberrations that are present to some extent in every eye regardless of refractive error (2,3,9). As illustrated in Fig. 3.4, a theoretical diffraction-limited visual system would have significantly better sensitivity at low frequencies, rather than the drop-off that is actually observed.

Clinical assessment of CS includes the full gamut of available subjective and objective techniques and procedures. As with testing of other aspects of visual function (e.g., VA, color vision, and flicker sensitivity), the ability of the patient to perform the test must be taken into account. For example, it would be useless to ask an infant to read aloud the letters on a standard acuity chart, although most adult patients know exactly what is expected of them and can perform the test easily and quickly.

Tests of CS can be grouped into several categories, and most tests will fall into multiple categories, depending on the nature of the stimuli and the procedure used to gather the data: