Fig. 4.1
Individual lamella showing orientation of the collagen fibrils
We then postulate that a strain energy density W for an individual lamella takes the form [4]
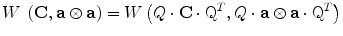where C is the right Cauchy–Green deformation tensor, a is the orientation of the lamella (and also of the collagen fibrils within the lamella) relative to a fixed Cartesian coordinate frame, and Q is an arbitrary orthogonal transformation tensor. This implies that W is a function of five invariants:
where λ is the stretch of collagen fibers oriented with direction a.
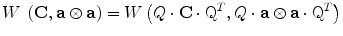
The strain energy density is assumed to be additively decomposed into three parts:
1.
The part W T describes the isotropic ground substance.
2.
The part W L describes the collagen fibrils with orientation a.
3.
The part W Q describes the fibril–fibril cross-linking and fibril–ground substance interaction.
We have postulated a model of the form:
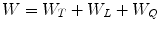
Where
![$$ \begin{array}{cc}\hfill {W}_T\hfill & \hfill \kern-2.7em =\frac{\mu_T}{2}\ \left({I}_1-3\right)-\frac{\mu_T}{2}\\ln\ {I}_3+\frac{\lambda_T}{2}{\left( \ln \sqrt{I_3}\right)}^2\hfill \\ {}\hfill {W}_L\hfill & \hfill \kern-2.1em =\frac{1}{4}\ \beta \left[{\displaystyle \int {e}^{\upgamma}\left({I}_4-1\right)d{I}_4-1}\right]+d\left({I}_4-1\right)\hfill \\ {}\hfill {W}_C\hfill & \hfill \kern-1em =\frac{1}{4}\ \alpha \left({I}_1-3\right)\left({I}_4-3\right)+\frac{1}{2}\left({\mu}_L-{\mu}_T\right)\left({I}_5-1\right)\hfill \end{array} $$](/wp-content/uploads/2017/03/A272372_1_En_4_Chapter_Equc.gif)
and where λ T , μ T , μ L , α, β, and d are constants. Only five are independent (see below), and values for these must be identified from appropriate experiments.
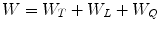
(4.1)
For hyperelasticity, the stress may be found from the gradient of the strain energy density with respect to its conjugate strain. This tells us that
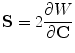
where S is the second Piola–Kirchhoff stress, and C is (as above) the right Cauchy–Green deformation tensor. For our model, the stress in the lamina is found from
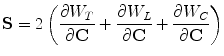This provides us with a rather general and powerful model for a lamella.
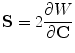
(4.2)
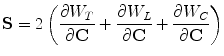
1.2 Corneal Model with Rotational Averaging of Lamella
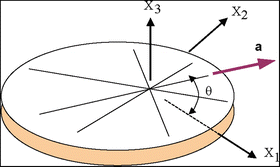
Since lamellae make large angles with adjacent overlying and underlying lamellae and since they have random orientation in the corneal plane, we introduce a rotational averaging (Fig. 4.2) of the energy density function of the form
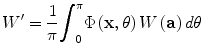where each vector a provides the dependence on θ (in fact θ6 = arctan (α02/α1)), and Ф(θ) is a weighting function of θ which can be used to describe nonuniform angular distribution of lamellae in different regions of the cornea (e.g., preferential orientation at the limbus). Since the ground substance has been assumed isotropic, its contribution will be independent of the angular averaging. Accordingly, we set
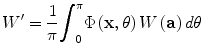
![$$ \begin{array}{cc}\hfill {W}^{\prime}\hfill & \hfill \kern-1em ={W}_T+\frac{1}{\pi }{\displaystyle {\int}_0^{\pi}\Phi \left(\mathbf{x},\theta \right)\left[{W}_L\left(\mathbf{a}\right)+{W}_L\left(\mathbf{a}\right)\right]d\theta}\hfill \\ {}\hfill \hfill & \hfill \kern-10.25em ={W}_T+{W}_L^{\prime }+{W}_C^{\prime}\hfill \end{array} $$](/wp-content/uploads/2017/03/A272372_1_En_4_Chapter_Equf.gif)
Fig. 4.2
Setup for angular averaging of lamella properties
For uniform distribution of the fibrils, we will use
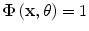
See [5] for nonuniform distribution of the fibrils.
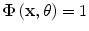
(4.3)
The new constitutive equation for stress is now
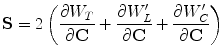The above theory has been implemented using the finite element method.
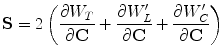
2 Calibration Studies for the Corneal Model
2.1 Introduction
We have used published experimental and clinical data as resources for identifying material parameter values as well as for verifying the model. The scope of this work is as follows:
1.
ALK for hyperopia (Phases I and II)
2.
Inflation tests on enucleated eyes (Phases I and II)
3.
Normo-hydrated regional strain inflation experiments of Hjortdal
4.
Radial keratotomy
5.
VISX-sponsored profilometry study
We have found that the inflation tests of Hjortdal, controlling the hydration by using a solution of Dextran and keeping the corneal thickness constant during the experiment, provide a particularly useful data set and one that shows the considerable “stress stiffening” of the cornea. The profilometry study has promise but requires more work. In this section, we review results and conclusions from the calibration studies with the exception of profilometry which is discussed in Sect. 4.4.
2.2 Calibration with ALK-H and Inflation Tests
Our first attempt (Phase I) was to calibrate the model with a lamellar procedure, such as ALK for hyperopia, where the mechanical response is evident and desirable. A normal cornea is considered spherical with 7.8 mm of radius of curvature and 0.5 mm of apical thickness. From the nomograms of microkeratomes for ALK (see Manche et al. paper in JRS), it is found that a normal cornea with a flap thickness of 300 μm produces a 1 D of correction (steepening) and more for deeper laps.
Stay updated, free articles. Join our Telegram channel
Full access? Get Clinical Tree
