Fig. 3.1
The dioptric plot is color-coded so that steep and flat areas on the cornea can be easily visualized. An eye with irregular astigmatism is shown
The corneal structural parameters are difficult to measure in vivo. Several authors [11–16] present values for the Young’s modulus and the Poisson’s ratio for some layers of the cornea and sclera.
In order to introduce the corneal geometry of each patient, we developed an interface with the corneal topographer and a preprocessing stage to reconstruct the spatial geometry from curvature data. The considered criterion to determine the error in the reconstruction was the corneal topographer resolution (±0.25 D). The elevation z was obtained in each meridian by solving the differential equation
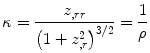
where z ,r and z ,rr are the first and second derivatives in radial direction.
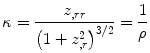
(3.1)
This interface with the corneal topographer has the advantage to allow reconstructing the corneal geometry in each patient without any geometrical simplification (as the sphere–cylindrical corneal shape assumption). Previous works used this assumption [14–20]. Moreover, both central and peripheral refractions are considered.
3 Finite Element Analysis
A structured four-layer mesh with isoparametric solid elements was considered. Linear interpolation and linear elastic and isotropic material are used to represent the cornea. Transverse isotropy was neglected, since we assume stresses in the perpendicular direction to the corneal plane are negligible when compared with stresses in the corneal plane. These assumptions were stated by following the Woo and Kobayashi studies [12].
In order to set the material properties of the cornea, different authors, as seen in Chap. 2 [11–16], present values for Young’s modulus and Poisson constant for the stroma and sclera. In a preliminary work values like 3 MPa and 0.48 were introduced in a finite element model, respectively.
Since the corneal model involves a portion of the eye, it is necessary to take special considerations in the boundary conditions of the model [18]. Since collagen fibrils at the limbus are oriented circumferentially (whereas they are oriented randomly in the cornea), we have considered the cornea to be hinged at the limbus as a boundary condition.
We inflate the unincised and incised models and subtract the curvature between them to obtain the final result. This procedure was compared successfully with other methods that disinflate iteratively the unincised model to obtain the initial unpressurized model.
3.1 Generation of the Incision
Incisions with diamond knife do not remove tissue and should not perforate the cornea, keeping the Descemet’s layer intact. The gape is afterward filled with healing tissue whose properties are different from the corneal tissue.
Some surgical techniques use variations in incision depth to obtain different refractive changes. The radial keratotomy for myopia, the Lindstrom arcuate technique for astigmatism, and the Arciniegas parallel technique for myopia and astigmatism are simulated [14]. These techniques perform incisions to maximum depth (90–95 % of the corneal thickness).
3.2 Generation of a Curvature Map
The structural analysis allows to observe geometrical changes and stress concentration zones. However, the ophthalmologist evaluates the surgical results from refractive changes in the corneal structure. Usually, he verifies the refractive changes by measuring the corneal curvatures with the keratometer, an optical instrument that measures four points at the corneal central zone and determines curvature from the sphere–cylindrical assumption of the corneal shape.
By incorporating a map of corneal curvatures, the refractive surgery can be analyzed broader (Fig. 3.2). The corneal topography allows the detection of irregular astigmatism appearing after the surgery. In addition, the paracentral and peripheral surgical effect is visible.
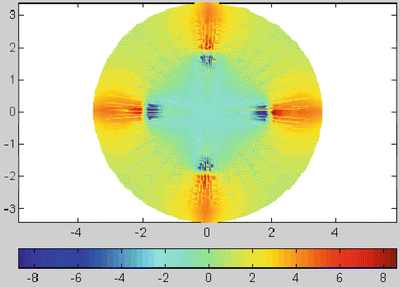

Fig. 3.2
After finite element analysis, a topographical map is calculated from the deformed shape. In the color plot, it is shown the difference in refraction from the presurgery map. The central zone shows a negative change of -2 D (flattening). In the incisions, the refractive change is higher
The axial curvature radius is calculated by fitting a circumference with three successive points in a meridian. By this way, we are able to compare the corneal topography after a surgical simulation with that measured after a real surgery, allowing to validate the model 3 y 4. This method is more powerful than those employed in other works [17–20] which calculated refractive changes in the cornea, by fitting an ellipsoid or paraboloid in the central zone (limiting the analysis to patients with regular astigmatism) [21].
4 Parametric Study of Radial Keratotomy
In order to validate the proposed technique, we first studied the sensitivity of a simulation of 4-incision radial keratotomy to variations in the intraocular pressure; surgical parameters, i.e., the incision length, the optical zone diameter, and the incision depth; and material parameters, i.e., Young’s modulus and Poisson’s ratio. We intended to validate with clinical and experimental results. In Fig. 3.9 it is shown the finite element mesh of the simulated 4-incisions radial keratotomy and the modulus of displacement is represented by a colored scale.
4.1 Relation with the Incision Length
The changes in curvature with variations in incision length were analyzed, by regarding the curvature radius in the astigmatism axes (0°, 90°) at 0.7 mm from the apex (Fig. 3.3). The optical zone was 2 mm, and four radial incisions were performed in the axes 0°, 90°, 180°, and 270°.
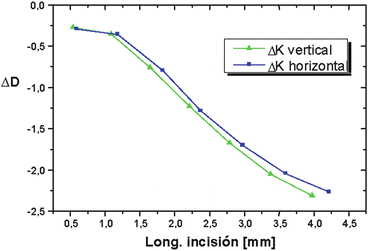

Fig. 3.3
Relationship between the incision length and the change in the keratometric refractive power for incisions with an optical zone of S mm and incision depth of 99 % of the thickness. The curvature is calculated in a diameter of 1.5 mm from the apex in the vertical and horizontal meridians
In general, a change in the length of the incision produces a change in the refraction by increasing the radius of curvature (flattening) in the central zone. The change decreases with longer incisions.
4.2 Relation with the Optical Zone
For a 7 mm incision length, the optical zone diameter was varied from 3 to 4 mm. We did not find a substantial change for incision of equal length having different clear zones between 3 and 4 mm in diameter.
We found a decrease in the refractive change when increasing the optical zone as expected (Fig. 3.4). Results were compared with the work of Pinsky et al. [20]. We found a general agreement in medium and large optical zones, but results differed for the smallest optical zone case since we are measuring the keratometric curvature which employs five points (2 in horizontal meridian, 2 in vertical meridian, 1 at apex) to calculate curvature instead of a spherical within a 3.00 mm zone used by Pinsky et al. [20].
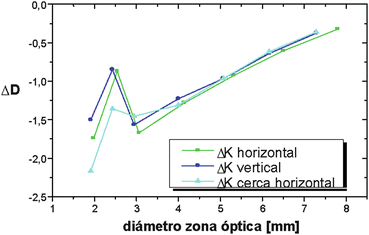

Fig. 3.4
Relationship between the diameter of the optical zone and the change in the keratometric refractive power for incisions with an incision length of 2.3 mm and incision depth of 99 % of the thickness. The curvature is calculated in a diameter of 1.5 mm from the apex in the vertical and horizontal meridians. For an optical zone lower than 2.5 mm, the incision produces distortion in the calculation of the keratometric curvature
4.3 Relation with Incision Depth
The increase in the incision depth produces greater flattening, almost linearly by the four-incision pattern (Fig. 3.5). Increasing the number of incisions would produce nonlinear variations. The elastic modulus and Poisson’s ratio were 3 MPa and 0.45, respectively.
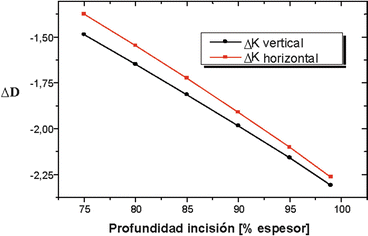

Fig. 3.5
Relationship between the incision depth and the change in the keratometric refractive power for incisions with an optical zone of S mm and incision length of U mm. The curvature is calculated in a diameter of 1.5 mm, from the apex in the vertical and horizontal meridians
4.4 Effect of the Young’s Modulus
We varied Young’s modulus from 0.6 to 15 MPa, in the eyes with 4 radial incisions. The Poisson’s ratio was 0.45. We present in Fig. 3.6 the radius of curvature measured in the apex, 3 and 5 mm from the apex vs. the elastic moduli in MPa.
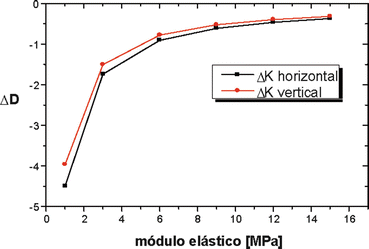

Fig. 3.6
Relationship between the elastic modulus and the change in the keratometric refractive power for incisions with an optical zone of S mm, incision length of U mm, and incision depth of 99 % of the thickness. The curvature is calculated in a diameter of 1.5 mm from the apex in the vertical and horizontal meridians. For stiffer corneas (older), the effect of the surgery is low
We found the lower the elastic modulus, the greater the correction. For values of elastic modulus greater than 11 MPa, the correction is smaller. This could be correlated with the stiffening age dependence reported [14].
4.5 Relation with the Poisson’s Ratio
The variation with the Poisson’s ratio was studied (Fig. 3.7). We found a negligible effect of the Poisson’s ratio from 0.2 to 0.4. The elastic modulus was 3 MPa.
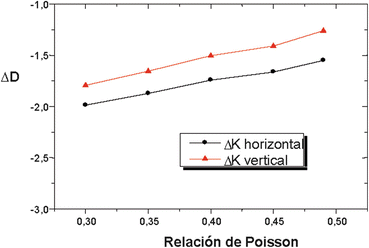

Fig. 3.7
Relationship between the Poisson’s ratio and the change in the keratometric refractive power for incisions with an optical zone of 2 mm, incision length of 2.3 mm, and incision depth of 99 % of the thickness. The curvature is calculated in a diameter of 1.5 mm, from the apex in the vertical and horizontal meridians
4.6 Relation with Intraocular Pressure
It was found that the effect of surgery increases with the intraocular pressure (Fig. 3.8). High eye pressures (>25 mmHg, like in glaucoma) present changes of 1–2D greater than in the physiological range (15–20 mmHg). The elastic modulus and Poisson’s ratio were 3 MPa and 0.45, respectively.
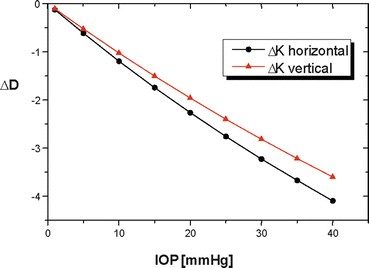


Fig. 3.8
Relationship between the intraocular pressure and the change in the keratometric refractive power for incisions with an optical zone of 2 mm, incision length of 2.3 mm, and incision depth of 99 % of the thickness. The curvature is calculated in a diameter of 1.5 mm from the apex in the vertical and horizontal meridians

Fig. 3.9
A colored graphic representation of the modulus of displacement (factor scale × 15). The horizontal incision gap is more pronounced than the vertical ones because of the different corneal diameters
5 Discussion
In this work, a structural model of the human cornea based on the finite element method was described. SAMCEF was used to perform the model preparation and the linear static analysis.
The geometrical model of the cornea considered in this work describes any type of ametropias, as well as any kind of pathologies which alter the corneal geometry. There were not geometrical assumptions, like symmetry axes, or revolution surfaces. Structural parameters resulting from a material homogenization performed by Hanna et al. were used. It was considered a linear behavior of the material binding analysis to low intraocular pressure (13–20 mmHg, which is the range of normal pressure for the surgical technique). By considering only a static analysis, the variations in the corneal parameters over time are not taken into account. Further studies about the wound healing process are necessary.
The size of the mesh, as well as the local effect sensitivity, was determined with a criterion to minimize the computational cost. Due to the expensive cost of this technique, the reduction in the analysis time allowed the study of the variations of several parameters.
The refractive results of the variation of the characteristic parameters of the model determined that it behaves acceptably well, imitating the real behavior of the cornea at the same conditions. The result of comparing the simulation with a real surgery only confirmed the previous conclusion. The error was greater than the desirable (±0.25 D).
Although there are many considerations, the main sources of the difference could be assigned to the boundary conditions imposed, data measuring errors, and an insufficient refinement of the mesh. The last factor could explain the stiffness showed by the numerical model.
At the point of view of the numerical model, we estimate convenience to incorporate error estimation strategies and an automatic mesh refinement to represent adequately the strong gradients introduced in the incisions. Similarly, we estimate the necessity to perform a better validation of the material behavior model of the corneal tissue (i.e., in the prior months to surgery, a refractive change that could be associated to a relaxation phenomenon was observed).
The results of this study are part of an interdisciplinary work between physicians and engineers. By integrating different contributions of the disciplines, like the engineering and the medicine, it is possible to reach fruitful results in the biomedical research area.
6 An Exponential Hyperelastic Material Model for the Corneal Tissue
The biomechanical response of the cornea in surgical procedures has been described mostly for radial keratotomy by measuring local deformations [22–24]. Others have used finite element models with different assumptions regarding corneal geometry and material properties. Some have assumed that the cornea is a homogeneous linear elastic solid [21, 25, 26], nonlinear elastic [17, 24, 27, 28] solid, and a nonhomogeneous membrane [20].
Attempts to verify the models have been done with inflation tests [28] in hydrated corneas and with local deformations [24] in normo-hydrated corneas. The relationship between corneal strain and intraocular pressure was found to be nonlinear, showing a typical stress-stiffening behavior. A material model by Woo et al. [12] has been used to account that nonlinearity [24, 27, 28].
The anisotropy of the cornea is evidenced by its microstructure as a reinforced composite with collagen fibers immersed in a jellylike matrix of mucopolysaccharides. There have been attempts to account the anisotropy of the cornea, with transverse isotropy but since the cornea is also nearly incompressible [29] violates the restrictions on the elastic constants [Sutcu 1992]. Pinsky et al. modeled the anisotropy produced by the relaxing incisions in a thick membrane model. But local bending effects near the incision were found to be an important factor [23].
The hydration has a profound effect on the extensibility of the stroma [23], and viscoelastic properties have been measured in vivo after radial keratotomy [30]. A complete model of the cornea should take into account the poroelasticity, viscoelasticity, and anisotropicity of the cornea.
Hyperelastic models are appropriate for material and geometrical nonlinearities. Geometric nonlinearities appear in inflation tests as well as in refractive procedures like those involving the insertion of intrastromal rings. They are also suitable for further extension to anisotropy and inelasticity. There were attempts to use rubber-based hyperelastic models, like Mooney–Rivlin [28, 31] and Ogden [28], but they did not reproduce the high nonlinearity of the cornea.
A hyperelastic model is presented that accounts for the nonlinearity of the cornea, both material and geometrical, and is suitable for viscoelasticity [32] and poroelasticity. Inflations tests [28, 33] are proposed in hydrated and normo-hydrated corneas to obtain the material parameters of the model.
7 Exponential Models for Biological Tissues
Several authors proposed to use exponential material models to represent the nonlinear elastic behavior of biological tissues. For instance, Fung proposed the following strain energy:
![$$ W=\frac{\mu_0}{2\upgamma}\left[{e}^{\upgamma \left({I}_1-3\right)}-1\right] $$](/wp-content/uploads/2017/03/A272372_1_En_3_Chapter_Equ2.gif)
where /i 0 (shear modulus) and seven are positive material constants [34, 35]. Also, Woo et al. [12] used an exponential model, in small strains, to analyze the corneal stroma, sclera, and optic nerve:

where σ eff and ε eff are effective stress and strain, respectively, and α and β are material constants. Bryant et al. used a similar model and characterized its parameters in an inflation test after failing with the Mooney-Rivlin and Ogden models. This model accounts for the material nonlinearity but is not suitable for further developments of viscoelasticity, as it was proposed in [32].
![$$ W=\frac{\mu_0}{2\upgamma}\left[{e}^{\upgamma \left({I}_1-3\right)}-1\right] $$](/wp-content/uploads/2017/03/A272372_1_En_3_Chapter_Equ2.gif)
(3.2)

(3.3)
7.1 Hyperelastic Nearly Incompressible Exponential Model for the Cornea
A hyperelastic exponential model is proposed, with an integral of the exponential term, in order to have a simpler form in the stress and elasticity matrix, after differentiation. A second logarithmic term is added with the second invariant of the deformation tensor C (similar to the Hart–Smith model) and a third logarithmic term with the third invariant of the deformation tensor C to account the near incompressibility [36, 37].
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


