Fig. 6.1
Loading condition for tonometry
Several years ago, the tonometry has been reviewed due to some difficulties detected on its fundamentals: design of the equipment, theory behind its development, and suppositions in the measure [12, 15, 18–28]. The Goldmann tonometry as a standard was calibrated with healthy adult eyes [3, 29]; that’s why now, it is not recommended for application in children [1].
1.1 Tonometry Exam: Procedure
All contact tonometers work according to the same basis: Imbert’s Law [29, 30]. Imbert’s Law establishes that if we have a circular tissue with an insignificant thickness (elastic membrane behavior) loaded in its internal face (the sphere is filled with fluid), it is possible to measure the internal pressure, applying a variable force against the external face in a known area until equilibrium is reached. In this sense, the tonometer mechanism intends to flatten a corneal region producing a known circular area.
This law (or theory?) does not take into account any lateral forces (membranal forces) or capillary forces.
The tonometry has two principal methods: digital tonometry and tonometry by instruments. The digital tonometry is a subjective method due to the intervention of physician fingers. There is no theory supporting this method. The tonometry by instruments is divided according to the instrument: applanation tonometry and indentation tonometry.
Measurements by applanation tonometry and indentation tonometry have influence of age, ametropies, geometrical parameters (CH, CCT, ECR, ICR), and corneal material parameters (E). Those factors influence in the amount of force necessary to produce the applanation of the corneal surface that is in touch with the tonometer applanation cone. This information was considered in a very broad manner to design the tonometry devices and their procedures; that is why these devices preserve some inaccuracies.
The applanation tonometry is a technique studied and perfectioned by Goldmann [31]. The instrument developed by Goldmann is based on the Imbert–Fick law. This law applied the Fick–Maklakoff principle that corresponds to the same definition for engineering pressure (Pressure = Force/Surface). It is mounted on the slit lamp used by ophthalmologists. Goldmann used the Imbert law through the application of a variable force over a constant applanation area (diameter of 3.06 mm); this area is formed while the instrument touches the patient’s cornea.
The contact tonometer tip has a PMMA lens where there is a well-known circumscribed circular area; it is necessary to push the tonometer against the cornea to match this area with a flattened cornea. When this area is reached, the ophthalmologist makes a read of the apparatus related to the force necessary to flatten the cornea so it is possible to reach that preestablished area; IOP = F/A, where F is the force applied and A is the well-known area.
Barraquer [33] pointed out that where the IOP is measured through applanation tonometry, the applied force is variable, the flattened corneal surface is constant, and there is a minor displacement of volume of liquid.
In order to analyze all the forces participating in the applanation tonometry, it is important to consider that the cornea has an elastic force that rejects the applanation (N) and a lacrimal meniscus between the flat surface of the tonometer and the cornea, adhering the flattening surface to the cornea (Force M). This force needs to be added to the previous one as follows: (P)(S) + N = F + M, so P = (F + M − N)/(S), where (P) is the intraocular pressure, (S) is the flattened surface, (F) is the force applied in the tonometer, and (M) is the force in the meniscus [34].
1.2 Geometrical and Functional Parameters for Tonometry
The “calibrated dimensions” is the term used for all the geometrical characteristics for the human cornea and the applanation zone for the contact tonometer measurement. The calibrated dimensions are ECR of 7.80 mm, CCT of 0.520 mm, and flattened area of 7.35 mm2 [13]; according to Goldmann, any variation of these parameters will incur in a wrong measure for the IOP. The elasticity of the cornea was not considered for the development of the device (tonometers). The cornea was considered as an elastic membrane with an insignificant thickness.
1.3 Tonometry Devices (Indirect Measurement of IOP)
The tonometry has grown since the last 20 years. The former devices were based on mechanical actions, and, now, the tonometry is turning to a new kind of device directed to diminish the effects of flat areas, thick corneas, pain during the exam, covering of all ages, etc. If the reader wants a deeper study about tonometric devices, descriptions of all kind of devices are found on literature [3, 35, 36]. In the following paragraphs you will find a description of each device known until now.
1.3.1 The Goldmann Tonometer
Among several methodologies to determine the intraocular pressure (IOP), both invasive and noninvasive technologies, the Goldmann tonometry is considered the “gold standard” for this measurement as it is identified as the benchmark or reference pattern for any other measure determined as IOP.
During IOP measurement with the Goldmann tonometer (contact tonometer), it is necessary to highlight that the PMMA tip of the tonometer (Fig. 6.2) pushes the cornea (anterior-posterior movement) mechanically to generate a flat circular area on it (Fig. 6.3). The circular applanated surface corresponds to a circle of 3.06 mm of diameter. The procedure uses fluorescein to improve vision of contact area. If the fluorescein meniscus around the applanated area has a thickness of 1.80 mm (using the slit lamp with a zoom of ×10), M and N forces are supposed to be in equilibrium [34]. According to Goldmann, the force needed to applanate the cornea (measured in grams) should be multiplied by 10 to measure IOP in mmHg.

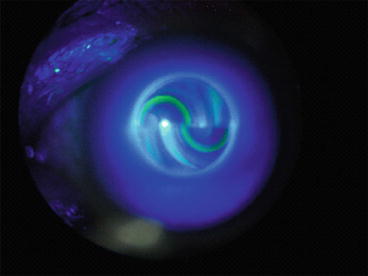

Fig. 6.2
The Goldmann tonometer slit lamp (source: Wikimedia Commons)

Fig. 6.3
Goldmann semicircles during tonometry (source: Wikimedia Commons)
When volume changes were checked inside the anterior chamber (and its influence on the IOP measurement), it results that there is no an important change (0.44 mm3) [1]. That is why it is considered that the IOP = IOPt (pressure measured by the tonometer). Stamper et al. [37] explained that pressure difference between IOP and IOPt due to volumetric changes is 3 % (IOPt > IOP). Woo et al. [38] developed a curve relating IOP vs. ocular volume changes; this curve showed that little changes in volume, expressed in microliters, generate little IOP variations for pressure values lesser than 20 mmHg [38].
Due to all these mechanisms, from the engineering analysis, it is relevant to consider corneal parameters as the elasticity modulus (considering the cornea as an elastic material) or stress–strain curves that define the mechanical behavior of the cornea for the applanation procedure. Also, it will be relevant to know the Poisson ratio for compressibility analysis and the geometrical parameters of the cornea (ECR, ICR, CCT, LCT, etc.).
According to the previous arguments, it is necessary to point out that this device and the theory behind it have certain limitations. This device should be only applied on corneas with specific geometries. In addition, due to the device was set according to human adult corneas, it is questionable its usage on children or elderly patients.
The Goldmann tonometer consists in a dynamometer mounted in a system that allows to work with both the ophthalmic slit lamp and the ophthalmic microscope. The object that contacts the cornea is the applanation cone. The cone is mounted in the arm connected to the dynamometer). At the cone tip (contact zone) there is an embedded lens (measuring prism), manufactured in PMMA (E = 3.00 GPa, ν = 0.45); over this lens there are several prismatic lenses that help to establish the exact applanation area corresponding to a diameter of two semi-rings of diameter of 3.06 mm each (total width for the tonometer tip is 7 mm; the contact zone is less than half of this diameter).
For the Goldmann tonometer, it is considered that the desired area of applanation is reached if the semi-rings get in touch in their inner portion at the off-center position (those rings move horizontally if the force is lowered or elevated). After the applanation area is reached, the reading of the dial in grams is multiplied by 10 to obtain the IOP in mmHg. The dial is aside the protective case for the dynamometer of the tonometer [37].
1.3.2 Pneumatic Tonometers (Pneumotonometer or PT)
This kind of tonometer changes the mechanical action for compressed gas. This is a portable device to measure the IOP.
Abbasoglu et al. [39] compared measures between the PT and the GAT. These measures were obtained after a PRK (photorefractive keratectomy). They found that the PT measures the IOP with confidence in each and every portion of the cornea after this procedure while the GAT underestimates the IOP in 2.40 ± 1.23 mmHg. They also identified that there is no influence of the CCT or the corneal irregularities on the measurement of IOP by means of the PT.
1.3.3 Rebound Tonometers
These tonometers eject a probe against the cornea (actio–reactio law). The probe is made with plastic, but it has a conductor material; the conductivity is necessary to eject the probe and to measure the movement in and out the tonometer. The IOP is determined due to the change of voltage induced in the probe movement. It was designed for a fast exam; any anesthetic or preparation is not necessary (Fig. 6.4).
1.3.4 Others
Pascal dynamic contour tonometer (DCT): The DCT is an applanation tonometer that adapts to the corneal curvature. This device is portable (Fig. 6.5). Kniestedt [40] and Kotecha et al. [25] identified that the DCT and the pneumotonometer showed less dependency on CCT related to the GAT measures.
Fig. 6.5
Exam using the Pascal dynamic contour tonometer (Source: Wikimedia Commons)
Reichert’s ocular response analyzer (ORA): This device reports information about the corneal hysteresis; this is an additional biomechanical parameter to consider due to the impact of the mechanics of the tissue and its independence related to the corneal geometry.
Lanza et al. [41] concluded in their research that the DCT or the ORA will be in the future the standard for tonometry due to their independence in the geometrical parameters that affects the Goldmann tonometry and its coherence with manometric measurements [42].
Diaton tonometer: The Diaton tonometer measures IOP through the eyelid and with no damage to the cornea. It is portable and easy to use (Fig. 6.6). There are reports comparing its results against the GAT and other devices.
Fig. 6.6
Exam using Diaton transpalpebral tonometer (Source: Wikimedia Commons)
Tonopen
2 Direct Measurement of IOP: Experimental Research
Experimentation is an important task in research activities. This activity relates the biomechanical behavior of the biological tissues with their material theoretical models. A proper characterization ensures an analytical model for certain procedures o extreme conditions during surgery.
For the tonometry, there are two types of experimentation: tensile tests or inflation of corneal buttons to determine the material properties for the cornea and sclera, and direct IOP tests by manometry.
2.1 Research in Animals
Due to the difficulty to find human tissues to perform mechanical tests, some researchers performed tests on animals to compare their mechanical properties with the corresponding of the humans.
Zeng et al. [43] performed tests on porcine corneas. They found that the average elasticity modulus for the porcine corneas is almost the same of the elasticity modulus for the human cornea (3.81 vs. 3.70 MPa).
DiSilvestro and Suh [44] compared three methodologies to validate a biphasic poroelastic model (BPVE: biphasic poro-visco-elastic model) in articular cartilage. They performed tests such as unconfined compression, indenting, and confined compression. Each prediction was performed through material parameters obtained from fitting curves of unconfined compression tests. The protocol for the tests includes a preparation of samples with pre-stretching of 10 % of the original length. This preparation assures that the tissue is ready to behave as a linear material.
Since the decade of 1960 leporids have been widely used for experimentation in ophthalmology [34, 45–47]. This experimentation developed through the determination of the true IOP by manometry. Sears [45] performed several manometry tests on sedated rabbits while the IOP was altered by different means (e.g., tearing of the iris).
Iinuma et al. [46] plotted the changes on IOP due to a constant load over the rabbit cornea. This kind of research has the objective to recreate the tonometric conditions. This work performed tests on rabbits and enucleated eyes from humans. The relevance of this research implies that give answer to incongruences for IOP determined with manometry. The manometry has several sources of error like the place where the eye is cannulated, the fluids and equipment used.
2.2 Research in Human Eye
Tensile tests and pressure test are the preferred tests in human eyes. Below, there is a review of documentation related to these tests and the computational models developed to understand the structural behavior of living tissues like the cornea. Non-linear behavior of these tissues make difficult the validation of these computational models.
3 Biomechanical Models of the Eye for Tonometry
Several researchers had performed tests on ocular tissues to report corneal mechanical behavior (stress–strain curves). The most important are uniaxial tensile strength test and inflation test in corneal buttons. For tonometry, applanation and indentation tests are of special interest to determine corneal rigidity not for membrane but for transversal loads.
Friedenwald was the first researcher that correlates the geometrical parameters for the eye with a “rigidity” coefficient [48, 49]. He designed a “plethysmographic” camera. This camera was able to detect changes of fluid volume in the anterior chamber due to corneal applanation. He also documented the influence of this procedure on the iris and the ciliary processes. To accomplish this, he replaced a known amount of aqueous humor for a gas bubble; for each test, while a tonometry measurement is performed, there is an extraction of a little amount of gas. This test is repeated along a timescale. Friedenwald concluded that a high rigidity is found in an eye with a low curvature radius (a flat eye suffers higher strains). He also established a calibration scale for the Goldmann tonometer. All his tests were performed in pig eyes, cat eyes, and rabbit eyes.
Schwartz et al. [50] determined the elasticity modulus for the epithelium. They studied the mechanical influence of this layer on applanation tonometry.
Some researchers as Armaly [51], McEwen [52], and Kronfeld [53] found that the corneal rigidity diminishes as IOP is increased. This statement was reevaluated by Orssengo and Pye [13] several years after.
Greene [54] performed inflation tests with cornea buttons. This study tried to find the mechanical properties of the cornea, specifically for epithelium and endothelium and their influence on the myopic refractive illness. He concluded that neither epithelium nor endothelium had any responsibility on corneal mechanics.
The mechanical properties for the cornea in compression were studied by Battaglioli and Kamm [55]. They found that the elasticity modulus for the cornea loaded in a radial direction was one hundred times smaller than the elasticity modulus for the membrane situation (circumferential stresses). The Poisson ratio was reported to vary from 0.46 to 0.50. Compression tests were performed in small cylindrical sections submitted to a compressive load of 200 Pa; after a stabilization time of 30 min, force and strain were measured (Fig. 6.7).
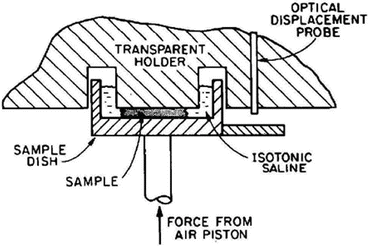

Fig. 6.7
Section cut for the positioner of the scleral sample in compression tests (adapted from Battaglioli and Kamm [55])
Figure 6.8 shows a section cut for the positioner of the scleral sample in compression tests (Adapted from Battaglioli and Kamm [55]).
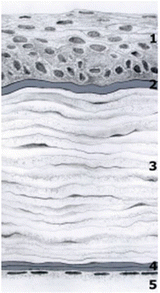

Fig. 6.8
Corneal layers. Section cut: (1) epithelium, (2) Bowman’s membrane, (3) stroma, (4) Descemet’s membrane, and (5) endothelium (adapted from [57])
In the following sections, we will present some analytical models for the corneal behavior accepted for tonometry.
3.1 Analytic Models to Represent the Corneal Material Behavior
For computational modeling, some authors [56] take into account the five layers for the cornea: endothelium, Descemet’s membrane, stroma, Bowman’s membrane, and epithelium (Fig. 6.8). Nevertheless, is widely accepted that the stroma is the main structure; it covers 90 % of the CCT (500 μm). The stroma is composed for collagen lamellae, ground substance, and keratocytes.
It is important to highlight that Bryant and McDonnell [58] developed models through finite element modeling with the objective to study the response of the cornea in the radial keratotomy. They developed three different models for each material considered: linear elastic isotropy, transversal linear elastic isotropy, and nonlinear isotropy. The geometric model considered was axisymmetric with mapped mesh. The mechanical properties for the material were obtained by experimentation with membrane inflation (human cornea buttons) and its comparison with nonlinear models with finite element analysis (Fig. 6.9). For linear models, the elasticity modulus varies from 0.79 to 0.83 MPa.


Fig. 6.9
In the same work, Bryant and McDonnell recalled some results from previous studies in regard to determining the elasticity modulus for the cornea: 0.025 MPa [59] for IOP of 10.0 mmHg and 17.0 MPa [60] for IOP of 100 mmHg. They concluded that the corneal stiffness increases at higher pressures. This observation is evident in the experimental curves for pressure displacement in Fig. 6.9.
Wang et al. [61] developed a technique to obtain the mechanical properties of the cornea through ultrasound. The samples of corneal strips were prepared with saline and dextran. The elasticity modulus for each preparation was 5.30 ± 1.1 MPa and 20.0 ± 0.1 MPa, respectively. The latter is similar to results for tensile tests reported for authors as Arciniegas and Amaya [4]. Wang et al. pointed out the causes of lack of consensus for the mechanical properties of the cornea:
Nonlinearity of the mechanical properties for the cornea: stress–strain curves
Quality of tissues: old tissues, altered tissues, or bad preservation of tissues
Test method: inflation tests and tensile tests
3.1.1 Linear Models
The elastic behavior is present in most of the structural materials. They are characterized by a linear proportion between stress and strain for the material. For many phenomena associated with corneal pathologies, it is considered an elastic behavior for the corneal material; nevertheless, there is no consensus about a modulus of elasticity for each individual (e.g., according to age). This supposition is valid, while certain conditions are accomplished: corneal deformation and load type.
For tonometry, where it is important to establish the relevance of each influential parameter, it is considered appropriate to employ a linear elastic model due to the short-term process and the low deformation determined as elastic.
Mow [19] developed the “sandwich shell theory” aiming to estimate and analyze the mechanical properties for the elastic cornea during applanation tonometry. This theory includes several assumptions as considering three layers in the cornea with linear mechanic behavior. Mow concludes that his theory could be applied to applanation tonometry because the displacements induced by the tonometer are small enough to consider the cornea as a linear elastic material.
Amaya y Arciniegas [62] performed several experiments (tensile tests on corneal and scleral tissues) to calculate the stiffness of the eye globe tissues (average elasticity modulus for adult human cornea and sclera, E = 20.0 MPa). They performed these experiments for high levels of load and deformation (yield stress for human cornea and sclera: 4.00 MPa). They concluded that stiffness decays with age (Fig. 6.10). Some of these arguments have been controverted nowadays; ElSheik et al. [7] demonstrated that stiffness is proportional to aging because of elastin loss. There is no consensus because there are no more conclusive reports; nevertheless, it is clear that it is not correct to use solely one elasticity modulus for the whole world population; it changes with age.
Pinsky and Datye [63] propose a model for the cornea where the structural responsibility is assigned to the stroma. They based their theory on the stromal microstructure and explained that the human cornea has flexural and shear rigidities that are insignificant compared with membrane rigidity. They proposed a biostructural model for the cornea as a thick shell where the tensile forces are resisted by collagen fibers embedded on the cell matrix. They consider a linear elastic model without time dependence.
Buzard [64] performed inflation tests to determine the elasticity modulus for the cornea. He found that secant elastic modulus is 7.58 MPa (constant) for IOP ranging from 25.0 to 100 mmHg.
Through ultrasound, it is possible to evaluate the particles’ vibration on the cornea [61]. Wang et al. considered that the cornea can be considered as a lineal material in a specific deformational state due to the low vibration perceived on the ocular tissues.
Anderson et al. [65] suggest in their work that it is possible to consider the cornea as a linear elastic material if the IOP ranges from 15.0 to 30.0 mmHg. The elastic parameters used for their modeling are referred to Orssengo and Pye [13]: E = 0.0229 × IOP and ν = 0.49. Dupps and Wilson [66] also recommend to use a Poisson ratio of 0.49 for biological tissues due to its noncompressibility condition and a solid matrix filled with fluid.
Hamilton and Pye [27] presented in their work that the elasticity modulus for a number of healthy young eyes is 0.29 ± 0.06 MPa. They performed a work where the Orssengo and Pye algorithm [13] is implemented and compared with experimental tests. The Poisson ratio was considered as 0.49. The authors stated that the IOP could be underestimated when the tonometry exam is performed in a cornea with a thick CCT due to its highly hydration. According to previous works [13, 18, 24, 27, 35, 59, 61, 67, 68] the elasticity modulus for the cornea varies from 0.10 to 57.0 MPa due to possible variation on tests conditions (there is no consensus about a standardized test). Authors also stated that the correction algorithms for the Goldmann tonometry that are based on CCT (solely) are incurring on errors for IOP estimation.
3.1.2 Multi-lineal Models
Kobayashi and Woo [69] made an important assumption that was implemented for the analysis of applanation tonometry. They stated that the corneal and scleral shells behave as an isotropic material when they are loaded on their situation of double curvature. The materials defined on this work are modulus of elasticity for stroma (E = 2.0 × 107 dyna/cm2 = 2.0 MPa), modulus of elasticity for sclera and for Descemet’s membrane (E = 5.5 × 107 dyna/cm2 = 5.5 MPa), and Poisson ratio (0.45). Nyquist’s research [70] was the source for some assumptions of this analytical study. Tonometry model developed by Kobayashi and Woo is depicted in Fig. 6.11.
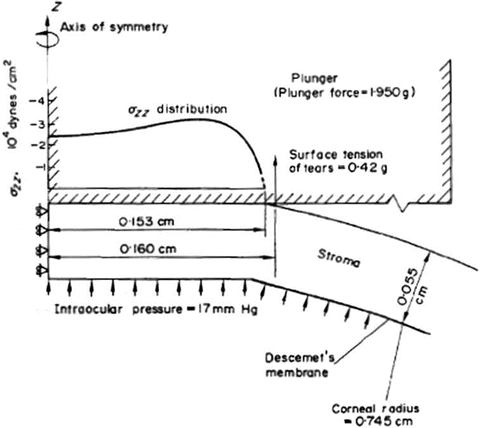

Fig. 6.11
Model for applanation tonometry. Stress distribution on the tonometer tip (adapted from Kobayashi and Woo [69])
One year later, Woo and Kobayashi [38] presented new information in regard to theories for modeling of corneal phenomena. Woo and Kobayashi assumed a modulus of elasticity for the corneal stroma of 2.0 × 105 dyna/cm2 (20 kPa) during the applanation tonometry; this modulus coincides with approximations performed by Goldmann [71] for this modulus.
Woo and Kobayashi [72] also developed a trilinear model for corneal material (Fig. 6.12). These models were developed through tests on pressurized corneal buttons of human eyes enucleated 1–3 days after donor decease. For the modeling of applanation tonometry for physiological conditions of IOP, there were considered the elasticity modulus for the flatten stroma (loading condition for the tonometry) combined with the trilinear model [38]. Surface tension due to lacrimal film is considered in this work as 0.42 g for a corneal diameter of 3.20 mm [50]. They suggest for the first time to use a solid filled with fluid for tonometric modeling (poroelastic model).
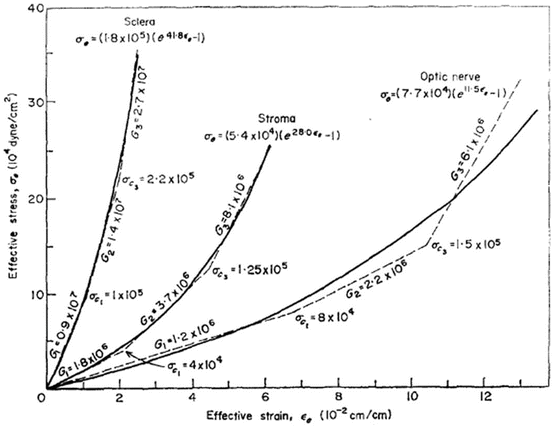

Fig. 6.12
Exponential approximation of trilinear stress–strain curves for ocular tissues (adapted from Woo and Kobayashi [72])
It is believed that the most accurate procedure to determine the mechanical properties of the cornea is through inflation tests. This procedure has a strong similarity with corneal state in situ. Bryant and McDonnell [58] performed inflation tests in intact and fresh human corneas. They found that nonlinear corneal behavior is connected with a material nonlinearity (not geometrical). Modeling the cornea through the finite element method allows to infer that the transverse linear isotropy is not capable to model the anisotropy that had been evidenced during tests. Also, a hyperelastic law does not fit to the rigid behavior of the cornea. They considered the Poisson ratio as 0.49. To build a model with a transverse isotropy, it is possible to conclude that the elasticity modulus through the corneal thickness is ten times lesser than the elasticity modulus on the plane.
3.1.3 Nonlinear, Viscoelastic, and Biphasic (Poroelastic) Models
The biologic materials are different from the rest of materials used in engineering. These materials (biologic ones) are characterized by phenomena as creep (or deformation through time) and stress relaxation. This phenomenon is related to the variation on time of load of deformation. If this behavior is implemented in a computational model, it will be more accurate.
It should be noted that the stroma, the bigger layer for the cornea, is composed of water (78 % in weight), collagen fibers (15 % wt.), and proteins, proteoglycans, and salts (7 % wt.). This composition rules the mechanical behavior for the cornea [73].
As stated in 3.1.2, Woo and Kobayashi pointed out the necessity to consider a fluid inside the solid structure of the cornea.
Vito and Carnell [74], as other researchers, also considered to model the cornea including several layers especially during tonometry. They assumed that each layer is free to slide one against other. Also, they consider large displacements (combined with rigidity changes). As a result of their work, they recommend to increase the study of boundary conditions for tonometry because of its effects on both stress and strain. As most of the soft tissues, the cornea is considered as nonlinear and viscoelastic. Nevertheless, it is possible to obtain a good approximation of tonometry with a linear model with a modulus of elasticity for the cornea of E = 2.00 MPa and for the sclera of E = 5.00 MPa.
The material properties for the biological tissues are modeled as poroelastic models constituted by two phases: solid and fluid. Also, these tissues are subjected to finite deformations during normal daily activities and in the physiological range [75]. About this research, it is highlighted that opposite to many porous materials in engineering, hydrated biological tissues overcome great deformations in short periods. These deformations occur during lab test conditions where it is difficult to represent the physiological conditions (loads and restraints) for the eye globe.
In the same work, Levenston et al. performed a simplified version of the theory and formulation of biphasic modeling. They also addressed several variational formulations for the biphasic problem (Lagrange multiplier form, penalty form, and augmented Lagrangian form); after that, they presented the finite element implementation and its description with numerical examples.
In the computational modeling of the cornea, where it is required that the material should be treated as viscoelastic, it is necessary to have information about the permeability of each corneal layer. Prausnitz and Noonan [76] published information about permeability of each layer for the cornea against different kind of medicines regarding to evaluate the effectiveness in drug delivery. These permeability values (in animals) are summarized as referent:
Minimum: 1.0 × 10−7 cm/s
Maximum: 1.0 × 10−3.5 cm/s
Average: 1.0 × 10−5 cm/s
Other values of permeability for the cornea to study drug delivery and through different methods could be found in literature [77–81].
Through tensile tests in porcine eyes [43], it is possible to conclude that the mechanical models for porcine cornea are not suitable for research in human corneas where viscoelastic phenomena should be considered. Both corneas have different behavior on time; both corneas have different mechanical properties and different fluxes inside and outside the cornea.
In the work of Katsube et al. [82] is presented a solid model filled with fluid. In their work, the authors explain why the intact cornea has a strong tendency to absorb water to regularize its normal function. They also explained the behavior of water inside the living cornea and its function to maintain a negative pressure (sub-atmospheric pressure; 50–60 mmHg below the atmospheric pressure). This negative pressure is called imbibition pressure. The swelling property of the cornea can change through corneal thickness due to several bio-chemical regions with different hydration properties.
Ethier et al. [35] presented a revision of the literature according to average values for the elasticity modulus of the corneoscleral shell. They stated a range of 5.00–13.0 MPa. In their research, they presented an explanation of the developed theories to explain the behavior of the corneoscleral material, including the biphasic theory; this theory takes importance due to the time-dependent behavior of the cornea (viscoelastic material). This description evokes the heterogeneity of the cornea and its highly anisotropic behavior including its nonlinearity.
Another contribution of Ethier et al. [35] was a development of an equation that represents the viscoelastic behavior for the cornea. This equation was derived from the stress relaxation technique (time dependent) on corneoscleral strips.
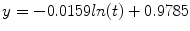
The simplest formulation for viscoelasticity is to consider a biphasic model for the cornea. To achieve this goal, it is necessary to perform formulations that set the coupling between solid and liquid phases composing the tissue. Prokofiev and Dunec [83] presented a simple methodology for poroelastic formulation in COMSOL package. This formulation coincides with the formulation presented at Rémond et al. [84].
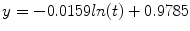
(6.11)
In poroelastic biphasic models, where it is considered the interstitial fluid, it is important to consider the barriers present in the cornea and the proper actions for its maintenance. This subject was treated by Dupps and Wilson [66]; they describe specific characteristics of the human cornea as: hydrophilic characteristic of the stromal glycosaminoglycans [85], imbibition pressure, corneal hydration level [86], stromal swelling pressure, and active endothelial transport [87].
The cornea is a complex anisotropic compound with nonlinear elastic properties including viscoelasticity [66] (Fig. 6.13). Dupps and Wilson refer that interlamellar shear strength is weaker than the corneal tensile strength; this situation grants the corneal stability and the mainly tensile stress state. They also identified that just the corneal stroma and Bowman’s membrane have collagen fibers (responsible of tensile strength); also, they found that Bowman’s membrane removal doesn’t affect the mechanical properties of the cornea (agreeing with [88]). This latter finding was possible through tensile tests and stress relaxation tests for corneal strips (Fig. 6.14).


Fig. 6.13




Nonlinear elastic properties for a corneal strip of 7 mm; 63-year-old patient (with permission of Dupps and Wilson [66])
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree