Fig. 9.1
Schematic input-output functions of NH (circles, HL = 0 dB) and HI (asterisks, HL = 31 dB) listeners, left ordinate. IO function for a signal processor with the desired inverse compression (squares), right ordinate
2.2 Compressive Gammachirp Filter
The block diagram of the compressive gammachirp filter (cGC) is illustrated in Fig. 9.2. The absolute Fourier spectrum, 
, is defined as
![$$\begin{array}{c}\left|{G}_{CC}(f)\right|=\left[{a}_{\Gamma }\left|{G}_{\text{T}}(f)\right|·\mathrm{exp}\left({c}_{1}{\theta }_{1}(f)\right)\right]·\mathrm{exp}\left({c}_{2}{\theta }_{2}(f)\right)\\ \text=\left|{G}_{\text{CP}}(f)\right|·\mathrm{exp}\left({c}_{2}{\theta }_{2}(f)\right)\\ {\theta }_{1}(f)=\mathrm{arctan}\left\{(f-{f}_{r1})/{b}_{1}{\text{ERB}}_{\text{N}}({f}_{r1})\right\}\\ {\theta }_{2}(f)=\mathrm{arctan}\left\{(f-{f}_{r2})/{b}_{2}{\text{ERB}}_{\text{N}}({f}_{r2})\right\}\end{array}$$](/wp-content/uploads/2017/04/A273038_1_En_9_Chapter_Equ00091.gif)
where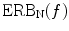 
is the equivalent rectangular bandwidth of average NH subjects. Conceptually, this compressive gammachirp is composed of a level-independent “passive” gammachirp filter (pGC), 
, which represents the passive basilar membrane, and a level-dependent high-pass asymmetric function (HP-AF), 
, that simulates the active mechanism in the cochlea. To realize the compressive characteristics, we defined the ratio 
between the peak frequency of pGC and the center frequency of the HP-AF as
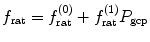
where 
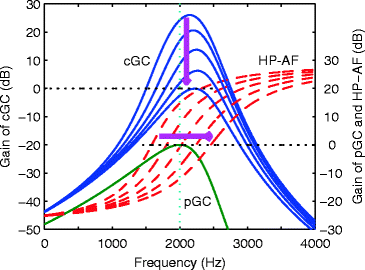
is the total level at the output of pGC in dB and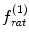 
is positive for compression. Figure 9.3 illustrates that the HP-AF shifts up in frequency (rightward arrow) and the peak gain of the cGC decreases (downward arrow) as the input sound level increases.
, is defined as(9.1)
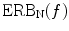is the equivalent rectangular bandwidth of average NH subjects. Conceptually, this compressive gammachirp is composed of a level-independent “passive” gammachirp filter (pGC), , which represents the passive basilar membrane, and a level-dependent high-pass asymmetric function (HP-AF), , that simulates the active mechanism in the cochlea. To realize the compressive characteristics, we defined the ratio between the peak frequency of pGC and the center frequency of the HP-AF as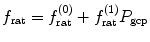(9.2)
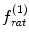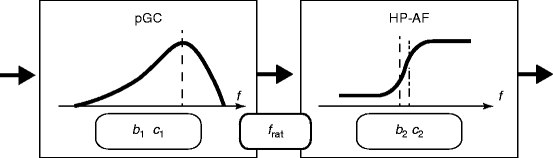
is the total level at the output of pGC in dB and is positive for compression. Figure 9.3 illustrates that the HP-AF shifts up in frequency (rightward arrow) and the peak gain of the cGC decreases (downward arrow) as the input sound level increases.Fig. 9.2
Structure of cGC. The relative position of pGC and HP-AF is defined by a level-dependent parameter, 
Fig. 9.3
The implementation of compression in the cGC. The arrows show the shift of the HP-AF and the gain of the cGC when the input sound level increases
2.3 Implementation of Inverse Compression
Inverse compression is produced by reversing the arrows in Fig. 9.3, thereby inverting the sign of 
. First, we define the center level for inversion, 
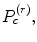as
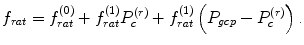
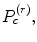. First, we define the center level for inversion, as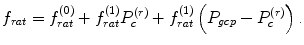By substituting 
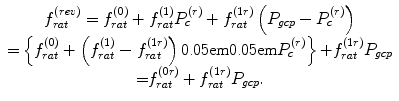
for 
for 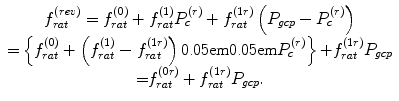(9.3)
