(23.1)
where
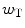 and
and 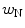 are, respectively, the decision weights on the target and the noise; μ Τ and μ Ν denote the nominal sizes of target and noise (before perturbation); β is a response criterion; and
are, respectively, the decision weights on the target and the noise; μ Τ and μ Ν denote the nominal sizes of target and noise (before perturbation); β is a response criterion; and 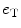 ,
, 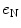 , and
, and  are zero-mean normal deviates representing various imperfections in the decision process (internal noise). The internal noise terms are taken to be independent of p T and p N and are so pooled to yield a single error term, e (a step justified by the fit of the model). The parameters of the decision rule are then estimated by regressing the listener’s trial-by-trial response on the values of p T and p N, where the influence of internal noise is estimated from the regression error, σe. In practice, the regression is performed using the glmfit routine of MATLAB v.7.0.1 with logistic link function,
are zero-mean normal deviates representing various imperfections in the decision process (internal noise). The internal noise terms are taken to be independent of p T and p N and are so pooled to yield a single error term, e (a step justified by the fit of the model). The parameters of the decision rule are then estimated by regressing the listener’s trial-by-trial response on the values of p T and p N, where the influence of internal noise is estimated from the regression error, σe. In practice, the regression is performed using the glmfit routine of MATLAB v.7.0.1 with logistic link function,![$$ \text{logit}[P(\text{Larger})]={c}_{0}+{c}_{1}{p}_{\text{T}}+{c}_{2}{p}_{\text{N}}+e,$$](/wp-content/uploads/2017/04/A273038_1_En_23_Chapter_Equ00232.gif)
(23.2)
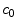 is an estimate of –β. (Note that the regression is performed on the type of response, not on whether the response is correct or incorrect.) The regression coefficients
is an estimate of –β. (Note that the regression is performed on the type of response, not on whether the response is correct or incorrect.) The regression coefficients 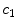 and
and  are finally used to estimate the decision weight on the noise relative to that of the target,
are finally used to estimate the decision weight on the noise relative to that of the target,
(23.3)
 = 0.
= 0.3 Application: Target Enhancement Versus Noise Cancellation
Here we consider a specific application of the approach designed to test different models of sound source segregation in noise, noise in this case referring to any sound source other than the target. These models generally fall into two classes: those based on enhancement of the target and those based on cancellation of the noise (Bregman 1990; de Cheveigné et al. 1995; Durlach 1963; Meddis and Hewitt 1992; Piechowiak et al. 2007). Much of the work aimed at testing these models has been done on the identification of concurrent pairs of harmonic and inharmonic vowels (see de Cheveigné et al. (1995) for a review). This work would seem to support a predominant role of noise cancellation; however, the tests are based on measures of performance accuracy which, as noted, may not best reflect the processes underlying segregation. In the present study, the relative contribution of target enhancement and noise cancellation is determined by the sign and magnitude of listener weights on the noise.
The listener’s task was size discrimination as in the example described above. A two-interval forced-choice procedure with feedback was used. The impact sounds of the membrane (target) and plate (noise) were synthesized using first-order analytic equations for the motion of these sources (Morse and Ingard 1968). The result in each case was a sum of exponentially damped sinusoids. For the membrane the frequencies were 500, 797, 1,068, 1,148, 1,327, and 1,459 Hz; for the plate they were 250, 700, 1,287, 1,495, 2,437, and 3,522 Hz. The amplitudes and decay moduli decreased proportionally with frequency beginning with a decay modulus of 0.2 s for the membrane and 0.4 s for the plate. The frequencies were perturbed from one presentation to the next as would correspond to changes in size. The perturbations were normally distributed in just-noticeable (jnd) units, with one jnd being equal to log(1.002) (Wier et al. 1977). The standard deviation of perturbations for the plate was fixed at 10 jnds; for the membrane it took on values σ T = 10–80 jnds, somewhat different for each listener. Sounds were played at a 44,100-Hz sampling rate with 16-bit resolution and were calibrated to be approximately 70 dB SPL at the eardrum (see Lutfi et al. 2008). They were delivered diotically over Beyerdynamic DT 990 headphones to listeners seated individually in a double-walled, IAC sound-attenuated chamber. Listeners were five students of the University of Wisconsin-Madison, aged 24–36 years. All had normal hearing sensitivity (ANSI S3.6-2004) and extensive previous experience with the task.
Now consider the predictions of the two classes of models for the noise weights in Eq. (23.1). Fundamentally, all noise cancellation models detect or recognize the target as a change from a baseline established by the noise. Probably, the simplest example is the old-versus-new (figure-ground) heuristic of Bregman (1990). Models that implement this process computationally involve some form of noise equalization followed by subtraction (e.g., Durlach 1963). For the present application, this can be shown algebraically to be equivalent to giving a negative weight to the noise in Eq. 23.1. We expect then that −1 <  < 0. Target enhancement models, by comparison, attribute noise interference to imperfections in the enhancement process that result in partial enhancement of the noise. A common example is the auditory filter model for tone-in-noise detection (Patterson 1976; Patterson and Nimmo-Smith 1980). These models predict the weight on the noise to be positive, so that we expect 0 <
< 0. Target enhancement models, by comparison, attribute noise interference to imperfections in the enhancement process that result in partial enhancement of the noise. A common example is the auditory filter model for tone-in-noise detection (Patterson 1976; Patterson and Nimmo-Smith 1980). These models predict the weight on the noise to be positive, so that we expect 0 <  < 1. (The analytic proof for both predictions is given fully in the recent publication of Lutfi and Liu (2011b).) Note that the decision model given by Eq. (23.1) also allows for the evaluation of a third alternative in which the noise simply serves to distract attention away from the target, without itself being given any weight (cf. Lutfi RA and Wightman FL 1996; Carlyon and Moore 1986; Werner and Bargones 1991). In this case
< 1. (The analytic proof for both predictions is given fully in the recent publication of Lutfi and Liu (2011b).) Note that the decision model given by Eq. (23.1) also allows for the evaluation of a third alternative in which the noise simply serves to distract attention away from the target, without itself being given any weight (cf. Lutfi RA and Wightman FL 1996; Carlyon and Moore 1986; Werner and Bargones 1991). In this case 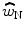 is expected to be near the optimal value of zero with less than optimal performance dictated by an increase in internal noise
is expected to be near the optimal value of zero with less than optimal performance dictated by an increase in internal noise  resulting from the distraction.
resulting from the distraction.
 < 0. Target enhancement models, by comparison, attribute noise interference to imperfections in the enhancement process that result in partial enhancement of the noise. A common example is the auditory filter model for tone-in-noise detection (Patterson 1976; Patterson and Nimmo-Smith 1980). These models predict the weight on the noise to be positive, so that we expect 0 <
< 0. Target enhancement models, by comparison, attribute noise interference to imperfections in the enhancement process that result in partial enhancement of the noise. A common example is the auditory filter model for tone-in-noise detection (Patterson 1976; Patterson and Nimmo-Smith 1980). These models predict the weight on the noise to be positive, so that we expect 0 <  < 1. (The analytic proof for both predictions is given fully in the recent publication of Lutfi and Liu (2011b).) Note that the decision model given by Eq. (23.1) also allows for the evaluation of a third alternative in which the noise simply serves to distract attention away from the target, without itself being given any weight (cf. Lutfi RA and Wightman FL 1996; Carlyon and Moore 1986; Werner and Bargones 1991). In this case
< 1. (The analytic proof for both predictions is given fully in the recent publication of Lutfi and Liu (2011b).) Note that the decision model given by Eq. (23.1) also allows for the evaluation of a third alternative in which the noise simply serves to distract attention away from the target, without itself being given any weight (cf. Lutfi RA and Wightman FL 1996; Carlyon and Moore 1986; Werner and Bargones 1991). In this case 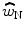 is expected to be near the optimal value of zero with less than optimal performance dictated by an increase in internal noise
is expected to be near the optimal value of zero with less than optimal performance dictated by an increase in internal noise  resulting from the distraction.
resulting from the distraction.Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


