This content presents to the neophyte ultrasonographer the essential nutshell of information needed to properly interpret ultrasound images. Basic concepts of physics related to ultrasound are supported with formulas and related to clinical use.
An understanding of ultrasound physics is essential for the proper interpretation of ultrasound images. Ultrasonic imaging relies on the reflection of sound occurring at the interface between tissues with different acoustical characteristics. Artifacts are common and can help or hinder diagnosis. To properly interpret the images, the ultrasonographer needs to have an understanding of the underlying sound wave. The intent of this content is to supply the minimum, the nutshell, of information needed to help a neophyte ultrasonographer. On first blush, the formulas may appear intimidating but they are meant to illustrate the physical relationships that affect and inform clinical ultrasound. The casual reader is invited to refer to them sparingly. For those who wish to know more, there are many in-depth analyses of ultrasound physics as applied in the clinical setting and several suggestions for additional reading are listed at the end of this article.
Sound waves
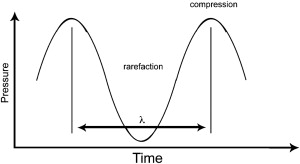
Sound waves are created by the propagation of vibrational energy through gas, liquid, or solid: molecules striking molecules. Measured from a single location, the mass molecular movements are detected as pressure waves alternating between compression and rarefaction as the vibrations pass by ( Fig. 1 ). Each repetition of the pressure wave is called a cycle. The two fundamental properties used to describe a wave are its wavelength and frequency.
Wavelength
Wavelength (λ) is the distance between like points on the wave occurring once per cycle. For a stationary observer, the time it takes for a complete wave to pass or a cycle to occur is called the wave’s period (T). The most common time scale used for sound waves is expressed in seconds, which means T is expressed in units of seconds per cycle. It is easier to use the inverse of the wave’s period, its frequency (ƒ), when comparing waves. For a wave with a period of T = 0.01 sec/cycle, ƒ = 1/T = 1/.01 = 100 cycles/sec. The combination of cycles per second is further simplified by using the common unit, the hertz (Hz), where 1 Hz equals 1 cycle/sec. For higher frequencies, kilohertz (kHz = 1000 Hz) and megahertz (MHz = 1,000,000 Hz) are used.
Sonic Range
The audible or sonic range is defined as 20 Hz to 20,000 Hz (20 kHz), the range of human hearing. By convention, frequencies above the range of human hearing are defined as ultrasonic. The most common frequencies used for diagnostic head and neck ultrasound range from 7.5 to 15.0 MHz. The choice of this range is a direct consequence of the physics, as discussed later.
Clinical ultrasonography relies on the measurement of reflected energy. Sound wave reflectance occurs essentially because of alterations in the speed of sound in different media or tissues. Understanding how the speed of sound changes is fundamental to understanding clinical ultrasound.
Propagation Velocity
The speed of a wave is called the propagation velocity. In the case of radiographs, the waves travel at the speed of light, which is 299,792,458 m/sec in a vacuum. Even the speed of light is not constant. It changes in denser materials because of propagating wave conversion into a hybrid of electromagnetic radiation and subatomic particle oscillations. The frequency of the light has effects at the quantum level, which in turn affect the speed of the light wave. Sound waves act at the molecular level. Frequency has no effect on propagation velocity for sound. The two are related by the following simple formula:
where c is the propagation velocity, ƒ is the frequency, and λ is the wavelength.
Two factors that do affect the speed of sound are the (1) density of the medium and (2) elasticity or stiffness of the medium as expressed in the following formula:
where c is the propagation velocity, C is the coefficient of stiffness, and ρ is the density of the medium.
Fig. 2 lists the propagation velocity of typical media encountered in the body. At first glance it might appear confusing that the propagation velocities increase in the denser media because the velocity is inversely proportional to the density (bone velocity > soft tissue velocity > air velocity). The reason is that the stiffness of these media increases much faster than their density does. In general, the speed of sound increases when going from a gas to a liquid to a solid.

Two clinical ultrasound measurements are directly dependent on the speed of propagation:
- 1.
Distance measurement
- 2.
Resolution.
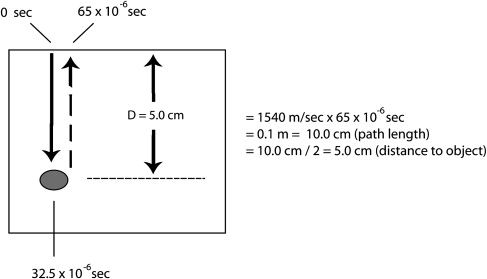
When measuring distance, the time required for sound to return to the transducer multiplied by its speed gives the distance ( Fig. 3 ). But, as noted, the speed of sound varies within different tissues based on density and stiffness. Because there is no way for ultrasound designers to know what tissues will be examined, ultrasound machines base distance calculations on an average speed for the expected tissues. The typical value used is 1540 m/sec, which is derived from averaging fat, liver, kidney, blood, and muscle. This value is a reasonable approximation for the majority of the soft tissues encountered in the neck. In an obese individual with a large percentage of neck fat tissue, actual and measured distances can be significantly different: 1450 (fat propagation velocity)/1540 (average tissue propagation velocity) = 6% differential.
The second clinical measurement depending on the speed of sound is the ability to resolve between two closely spaced points. The ability to distinguish between two points requires a wavelength of the same size or smaller than the distance between the two points ( Fig. 4 ). Resolution requirements quickly constrain the choice of frequency of ultrasound for clinical head and neck imaging. Recall the relationship between propagation velocity, frequency, and wavelength:
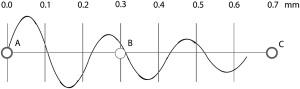
Using the average propagation speed in the head and neck and plugging in a frequency of 7.5 MHz yields
λ = c / f = 1540 m se c − 1 / 7 , 500 , 00 cycles · sec − 1 = 0.205 mm
Structures, such as lymph nodes and the parathyroids, are typically in the range of 3 to 4 mm in size. If there were no technical issues to consider, a single cycle of sound energy at 7.5 MHz would be more than adequate for resolving head and neck structures. Unfortunately, single cycle detection is impractical in reality. The transducer material used to create the sound energy acts like a bell. Striking it to start the ringing is simple, but like a bell it is difficult to dampen the induced vibrations after one cycle.
Acoustic Impedance and Reflectance
Clinical ultrasonography equipment relies on reflected sound measurements. Sound wave reflection occurs at the boundary between materials with different acoustic properties. The intrinsic property defining this difference is acoustic impedance ( Z ), which is the product of the density and the propagation velocity of a medium:
The greater the difference in impedances, the greater the amount of energy that is reflected. Because impedance is a product of density and propagation velocity, the greatest reflectance in the head and neck region is to be expected at air/soft tissue interfaces and bone/soft tissue interfaces. In contrast, ultrasound transducer gels closely match soft tissue impedance, allowing transmission of the sound energy through to the soft tissue with minimal reflectance.
If all reflected energy was returned to the sound detector, all differences between object appearances would be related to their relative impedance. But sound waves can be scattered in a manner where they do not return to the detector. Reflectors fall into 2 broad categories:
- 1.
Specular
- 2.
Diffuse.
A specular reflector is one that acts like a mirror. The classic specular reflector is smooth and large compared with the wavelength of the sound wave used to image it. Examples of specular reflectors include the diaphragm, the carotid artery, and fluid-filled cysts. Specular reflectors that are perpendicular to the sound wave’s propagation path reflect directly back to the transducer. Angled reflectors will reflect the sound energy away from the transducer leading to a loss of signal ( Fig. 5 ).
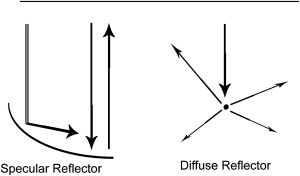
Diffuse reflectors are common in the head and neck region and account for the speckled patterns seen on ultrasound images. Sound energy is scattered rather than reflected in a coherent manner when the wavelength of the sound wave is larger than the size of the reflector (eg, 0.205 mm for a 7.5 MHz sound wave).
Attenuation
Diagnostic ultrasound imaging relies on the return of sound wave energy to the transducer. In addition to the scattering that occurs with diffuse reflectors and the angled reflectance caused by specular reflectors, another major source of energy loss is attenuation. Absorbance of the sound energy along the path of the wave limits the potential depth of penetration. Tissues absorb sound energy by converting the sound energy into heat. This conversion increases with the frequency of the sound wave and becomes the major factor limiting the depth of tissue penetration when using higher ultrasonic frequencies. As previously discussed, resolution sets a lower limit on the useful range of ultrasound frequencies for the head and neck region. Absorbance, the chief cause of attenuation, sets the upper limit.
Attenuation of the sound wave is measured in relative units based on the intensity levels of sound energy at two points along the propagation path. Intensity is a measure of how power is spread over an area:
Power ( in milliwatts [ mW ] / Area ( in c m 2 ) ) = I ( Intensity in mW / c m 2 )
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


