Refractive Error, Clinical Optics, and Contact Lenses
Jill E. Beyer
Deborah Pavan-Langston
I. Physical Optics Affecting Vision and Correction of Visual Refractive Errors
Wavelength of light. Electromagnetic radiation exists in many forms. The characteristic of the radiation that determines the form in which it is encountered is the wavelength. Long wavelengths are encountered as radio transmissions or radar; these emit a low energy. Short wavelengths are encountered as cosmic rays and x-rays; these emit a high energy. The visible portion of the electromagnetic radiation spectrum occurs between the ultraviolet and infrared portions, from 380 nm at the violet end of the spectrum to 760 nm at the red end.
Frequency of light waves. The frequency of electromagnetic radiation is the number of times a particular position on the wave passes a fixed point in a fixed interval of time. It is inversely related to the wavelength. For example, radio waves, which occur as long wavelength radiation, have a frequency of 104 cycles to 108 cycles per second (cps), whereas the visible part of the spectrum is in the 1014 cps to 1015 cps range and includes shorter wavelength radiation.
Velocity of light waves. The entire spectrum of electromagnetic waves travels at a speed of 3 × 108 m per second (186,000 miles per second) in a vacuum. The wavelength and frequency of light can be spoken of interchangeably because they are related through the following equation: wavelength × frequency = velocity of light = 3 × 108 m per second.
Index of refraction. Although the frequency of light does not vary with the density of the medium through which it is traveling, the speed is reduced in a dense medium. The ratio of the velocity of light in a vacuum to the velocity of light in a particular medium (n/n′) is referred to as the index of refraction for that medium. Because the frequency of radiation does not vary with the medium and the speed does, it follows that the wavelength in a dense medium is less than it is in air and is proportional to the change in speed. Each medium, therefore, has a different refractive index for a given wavelength. Short wavelengths, or blue light, are slowed down or refracted more than long wavelengths, or red light. This accounts for the chromatic aberration present in the eye or in single-element lens systems. The visible spectrum is defined in relationship to chromatic aberration and is described by the use of the C (red) – F (blue) line.
Quanta or photons. The energy in electromagnetic radiation is measured in units called quanta or photons. The energy of an individual photon is proportional to the frequency or inversely proportional to the wavelength. Therefore, the energy of a photon at 400 nm is twice as great as that of a photon at 800 nm. For example, red light is innocuous, ultraviolet light produces burns, and x-rays produce severe damage to tissues.
Loss of light by reflection or absorption. With respect to the eye, the light incident on the retina from a light source is decreased by loss from reflection or absorption at the cornea, lens, and retinal surfaces. Although the cornea is quite transparent from 400 to 1,200 nm, the crystalline lens does absorb some of the radiant energy, particularly short wavelengths. The young, healthy lens transmits incident light of 320 nm. Absorption at the blue end of the visible spectrum increases with age as xanthochromic (yellow-brown) proteins accumulate in the lens.
Some of the short wavelength radiation is also absorbed by the yellow pigment in the macular region of the retina.
Color of light. The physical stimulus that is responsible for the sensation of color is the wavelength of the radiation. Wavelength in the region around 430 nm produces a violet hue, around 460 nm blue, around 520 nm green, around 575 nm yellow, around 600 nm orange, and around 650 nm red. A mixture of wavelengths, such as that which occurs in sunlight, produces a white hue. It is also worth noting that objects appear as a particular color because they preferentially reflect wavelengths of that color and absorb the other wavelengths.
Reflection. When light rays strike a smooth surface, they may bounce off the surface, or be reflected, rather than pass through. Reflection from a polished surface is referred to as “regular” or “specular” reflection. This does not occur randomly but follows a simple rule—the angle of reflection is equal to the angle of incidence and lies in the same plane. The angle of reflection and the angle of incidence are measured relative to the surface perpendicular at the point of impact. When light is reflected, a plane or flat mirror reverses the direction of the light rays only and does not effect vergence, so no magnification, minification, or image inversion occurs. Convex or concave reflective surfaces can change the vergence of light rays and focus them, resulting in an altered image. This has a practical significance for spectacle wearers. Reflections from the ocular surfaces of corrective lenses can produce virtual images near the far point plane of the eye, images that can be annoying to the patient. The images can be eliminated by tilting the lenses or using an antireflective coating. The cornea can also be used as a reflective surface. The principal of keratometry depends on the anterior surface of the cornea, which acts as a concave mirror. By measuring the size of the reflected image, the cornea’s radius of curvature can be calculated. The cornea is also employed as a reflecting surface when checking it for irregularity with a keratoscope. By examining the reflected images of a series of concentric circles, one can check for distortion.
Refraction of light. When rays of light traveling through air enter a denser transparent medium, the speed of the light is reduced and the light rays proceed at a different angle (i.e., they are refracted). The one exception is when the rays are incident perpendicular to the surface (collimated or paraxial light). In this case the speed of the light is reduced, but the direction of the light is unchanged.
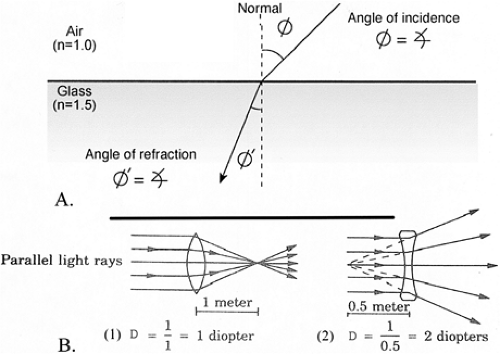
Snell’s law of refraction. The refraction of light at an interface is described whereby the angle of incidence and the angle of refraction are related to the density of the medium for a specific wavelength. When light passes from a medium of low density to a medium of high density, Snell’s law predicts that the light ray will be bent toward the normal, a line perpendicular to the surface at the point of impact (Fig. 14.1A). In other words, the angle of refraction is less than the angle of incidence when going from a low- to a high-density medium. Conversely, when light passes from a high- to a low-density medium (e.g., out of a tank of water into air), the angle of refraction is greater than the angle of incidence. By bending the surface of a transparent medium that has a high density, such as the cornea or a piece of glass, the angle of incidence can be altered, and by employing Snell’s law, the deviation of light rays by this altered surface can be predicted. All light rays from real objects diverge from one another; when these rays encounter a medium of high density, they can be made less divergent, parallel to one another, or convergent, depending on the shape and index of the refracting element or lens. By using simple formulas, the point at which the redirected rays come to a focus can be calculated quite easily.
Measurement of lens power. Lenses are measured in diopters (D). The power of a lens in D is the reciprocal of its focal length (f) in meters: D = 1/f. For example, a lens that focuses light from an object at infinity (parallel light rays or 0 vergence) at a plane 1 m beyond the lens is a 1 D lens (Fig. 14.1B). If it focuses the light at a plane 0.5 m beyond the lens, it is a 2 D lens: 2 = 1/0.5.
II. Types of Corrective Lenses
Spherical lenses have equal radii of curvature in all meridians.
Convex or plus lenses. By convention, high-density optical surfaces that are convex are referred to as plus lenses. They refract light rays so as to make them more convergent (or less divergent). Plus lenses of the same power can be made with a variety of radii, because it is the relationship of the two surfaces of a spectacle correcting lens that determines the power of the lens (Fig. 14.2A). A meniscus form, in which the front surface is more convex than the back surface is concave, results in the most desirable lens form for spectacles, because there is less spherical aberration over a wider area of the lens. A plano–convex-shaped plus lens will also reduce aberration. Plus lenses are used for the correction of hyperopia, presbyopia, and aphakia. When a nearby object is viewed through a plus lens, the object looks larger. If the lens is moved slightly from side to side, the object appears to move in the direction opposite to the movement of the lens. Plus lenses can also be identified by their physical characteristics; they are thicker in the middle and thinner at the edges.
Concave or minus lenses. High-density optical surfaces that are concave are referred to as minus lenses. They refract light rays so as to make them more divergent (or less convergent). As stated previously, it is the relationship of the two surface radii that determines the resultant power. Minus lenses can also be made in many forms (Fig. 14.2B). The most common design used in minus spectacle lenses is the meniscus, wherein the back or ocular surface is more concave than the front surface is convex. Myodisc lenses (biconcave) are used on patients who need very strong minus lenses. They induce less peripheral distortion, but offer a smaller focused central field than the meniscus lens. High-density plastic (polycarbonate) lenses have a higher refractive index than crown glass and may be used to reduce the thickness of high minus lenses. Minus lenses are used to correct myopia. When a nearby object is viewed through a minus lens, the object looks smaller. If the lens is moved slightly from side to side, the object appears to move in the same direction as the lens. Minus lenses are thin in the middle and thick at the edges.
Toric lenses are shaped like a section through a football. One meridian is more curved than all of the others, and the meridian perpendicular to the steepest meridian is flatter than all of the other meridians. In a toric lens, the meridians of least curvature and the greatest curvature are always at right angles to one another and are referred to as the principal meridians. Toric lenses are prescribed to correct astigmatism. Toric lenses can be identified by observing a vertical contour such as a window or door frame through the center of the lens and rotating the lens in a vertical plane (parallel to the surface that is being observed). If the lens is a toric lens, the edge of the vertical contour is broken or discontinuous in the area viewed through the lens. The image will also appear to rotate clockwise or counterclockwise as the lens is rotated back and forth. If the same vertical contour is viewed through the center of a spherical lens, it remains continuous when viewed within and outside the borders of the lens and does not appear to rotate when the lens is rotated. Toric lenses can be plus lenses, minus lenses, one principal meridian plus and the other minus, meniscus lenses, or they can be fabricated in a planocylinder form in which one principal meridian has zero optical power. Toric lenses are also referred to as spherocylinders.
Prisms. A prism is an optical device composed of two refracting surfaces that are inclined toward one another so they are not parallel. The line at which the two surfaces intersect is the apex of the prism. The greater the angle formed at the apex, the stronger the prismatic effect (Fig. 14.3A[1]). Because the two surfaces of a prism are usually flat, they alter the direction of the light rays, but not their vergence. An object viewed through a prism appears to be displaced in the direction of the prism apex, but the focus is not altered and no magnification or minification occurs. Prisms are usually prescribed to assist a patient with an extraocular muscle imbalance, which results in a deviation of one visual axis relative to the other, so that the patient may achieve single binocular vision or do so more comfortably. They may be oriented in the spectacle correction so as to produce horizontal, vertical, or both horizontal and vertical displacement, as needed. The strength of a prism is measured in prism diopters (pds). The prism power is equal to the displacement in centimeters of a light ray passing through the prism measured 1 m from the prism. (Each diopter displaces a ray of light 1 cm at a distance of
1 m.) Two prism diopters of displacement are approximately equal to 1 degree of arc.
Lensometers are precision instruments used to measure the spherical power, cylindrical (toric) power and the corresponding axis, and prism power, if present, of a spectacle or contact lens. Synonyms include: vertometer, vertexometer, dioptometer, and focimeter.
Technique. The lens to be measured is placed on the lensometer stage, and the power wheel is turned until the target mires are in focus. The mires cross each other at right angles; there are three lines in one meridian and one in the other. If the mires all focus simultaneously at a given power, no cylinder is present and the lens is completely spherical. The power is read directly off of the power wheel. The second wheel on the lensometer is an axis wheel, which can be rotated to turn the mires until they are lined up along the principal meridians of a lens containing a cylinder. Alignment is correct when the crossing lines are perfectly straight (not broken). The power wheel is then turned to focus the strongest plus power of the lens (single line meridian). When this is focused using the greatest plus power (or least minus power), the spherical power component is recorded. The power wheel is turned again to bring the weaker (more minus) meridian into focus (three-line target) and the cylindrical power component is noted as well as the axis of that meridian, which is read directly from the axis wheel. The lens prescription is the strongest plus power minus the difference in power between the two settings, and the axis of the cylinder is that of the more minus meridian, as indicated on the axis of the wheel.
Example of lensometer calculations
Strongest plus meridian reading: +4
Weaker plus meridian reading: +2.50
Axis of weaker meridian: 80 degrees
Final power: +4 = -1.50 × 80 degrees.
Strongest plus (weakest minus) meridian reading: -2
Weaker plus (stronger minus) meridian reading: -3
Axis of weaker plus meridian: 40 degrees
Final power: -2 = -1 × 40 degrees.
Plus cylinder prescriptions are less frequently used, but may be done by reversing the above technique. For example:
Weakest plus meridian: +1
Strongest plus meridian: +2.50
Axis of strongest plus meridian: 50 degrees
Final power: +1 = +1.50 × 50 degrees.
Conversion of minus cylinder prescriptions to plus or the opposite is carried out by reversing the sign of the cylinder, adding the difference between the two lenses, and adding 90 degrees to its axis, e.g., +3 = -2 × 20 degrees converts to +1 = +2 × 110 degrees.
Prism power is measured in the lensometer by reading the amount of decentration from the optical center cross mires. This is determined by counting the number of circles or lines on the eyepiece reticule away from center. For ground in prism, base-in is noted if the power center is located on the nasal side of the lens; base-out is noted if temporal. For induced prism, the difference between the patient’s pupillary distance and the lens optical centers determines the amount of induced prismatic effect. Prentice’s rule calculates the amount of induced prism.
III. Refraction Techniques
Refraction is the term applied to the various testing procedures employed to measure the refractive errors of the eye to provide the proper correction. Refractive error is by far the most common cause of poor vision. Fortunately, it is generally the easiest to treat.
Retinoscopy is an objective method of analyzing the optics of the patient’s eye to determine the refractive error. A retinoscope is a handheld instrument that the examiner uses to illuminate the inside of the patient’s eye and observe the light rays (reflected from the retinal pigmented epithelium and choroid) as they emerge from the patient’s eye. This process involves moving the streak of light back and forth across a series of lenses held in front of the patient’s pupil, resulting in a linear light reflex moving in the same (hyperopia) or opposite direction (myopia) as the light. The filling of the entire pupil with light that does not move indicates neutralization of the refractive error in that meridian and is the end-point reading for that meridian. The linear streak of light can be rotated 360 degrees through the pupil to examine different meridians of the eye. In the case of astigmatism, the retinoscope linear light must be empirically lined up along a principal meridian (the clearest light streak as the retinoscope light is rotated) and plus or minus lenses put up until movement of light in that meridian is neutralized and the lens power recorded. This is repeated in the meridian 90 degrees away for the second lens and axis. By knowing what lenses are required, it is a simple matter to calculate the amount of ametropia. Opacities of the media, tiny pupils, poor fixation by the patient, or distortion of the light reflex can all be troublesome. Prescribing lenses on the basis of retinoscopic findings alone can too often result in a prescription that is not well tolerated by the patient.
Subjective refraction is a tool whereby the examiner relies on patient responses to narrow the prescription further. Retinoscopy or automated refraction findings or habitual spectacle power may be the starting guide for subjective refraction. In the absence of astigmatism, the refraction is simply a matter of adding more plus or minus power until the patient reads his or her best visual acuity with the most plus or least minus power. In the presence of astigmatism, and to help test for it, the fogging technique is very effective (see Section VI.B.3.e). Refractions involving astigmatism are best refined by the Jackson cross-cylinder (JCC) technique (see Section VI.B.3.f), which may be done manually or by an automated refractor.
Automated refraction. In recent years, electronic microcircuitry and computer technology have combined to develop sophisticated instruments for refracting patients. In general, automated refractometers are highly accurate. The instrument must be properly in line with the patient’s visual axis, accommodation must be relaxed, the pupil must be of satisfactory size, and the media must be sufficiently clear. The primary role for these instruments is increased efficiency with which eye
care is delivered by obtaining the approximate refractive error, which then should be manually refined by the refractionist. For example, an automated refractor may indicate a cylinder axis of 15 degrees, but the patient’s habitual spectacles are at axis 10 degrees without discomfort. Often, it is wiser to give the axis 10 degrees with perhaps some sacrifice of visual clarity than axis 15 degrees, which is clear but feels “uncomfortable.”
Cycloplegic refraction. Cycloplegia is the employment of pharmaceutical agents to temporarily paralyze the ciliary muscle, thus stabilizing the eye’s accommodative reflex and allowing for the measurement of a definitive end point. Cycloplegic refraction is particularly useful in young patients with highly active accommodation. This ensures complete relaxation of the ciliary muscle, allowing for the accurate measurement of the ametropia in young hyperopes, thereby avoiding overcorrection. Methods of inducing cycloplegia include 1% cyclopentolate or tropicamide, one drop q5min for two applications in the office 20 minutes prior to refraction, or atropine 1%, one drop tid for 3 days before the refraction.
IV. Aberrations
Optical systems generally contain imperfections referred to as aberrations. Currently, the important aberrations in spectacle lenses are chromatic aberration, spherical aberration, radial astigmatism, and distortion.
Chromatic aberration. The index of refraction for any transparent medium varies with the wavelength of the incident light. This variation is such that blue light is refracted more than red light (Fig. 14.3A[2]). This accounts for the chromatic dispersion that occurs when white light is passed through a prism and a rainbow effect is produced. In a convex or plus lens, blue light is focused slightly closer to the lens than red light. The same is true of the human eye, in which blue light is focused slightly in front of red light.
Spherical aberration. In most discussions of optics, certain assumptions are made for the sake of simplicity. Higher-order optics become quite complex and contribute little to the understanding of basic measuring and prescribing of spectacles. So far, it has been assumed that all light rays from an object that pass through a lens come to focus at a single image point. A closer analysis reveals that this is true only for light rays that are paraxial (i.e., that pass through the center of the lens). Those light rays that are parallel to the axis but that pass through the periphery of the lens are usually refracted more than the paraxial rays. Peripheral rays will focus closer to the lens (Fig. 14.3B). Every object point on the axis of the lens will then be represented by a blur circle rather than a point focus. The size of this blur circle can be reduced by restricting the passage of light through the lens to the central portion, as is done when an object is viewed through a pinhole aperture. This same effect accounts for the increased depth of focus obtained when the iris diaphragm of a camera is reduced in size or when the pupil of the eye is constricted. Spherical aberration may produce a variable concentric retinoscopic reflex in patients with large pupils, with the peripheral portions of the pupil appearing myopic (against motion) while the central portion is at neutrality.
Radial astigmatism occurs when light rays pass through a lens obliquely. Instead of focusing a point of light as a point image, two linear images form at right angles to one another with a “circle of least confusion” between them. This form of aberration is of no great significance in the eye; however, it can create considerable blurring of the image formed by spectacle lenses.
Distortion is the result of differential magnification in an optical system. This occurs because light from some parts of the object is focused by the central portion of the lens, while other parts are focused by peripheral portions of the lens. In other words, the shape of the image formed does not correspond exactly to the shape of the object. For practical purposes, this is not a problem in the eye, but it can be troublesome in higher-powered spectacle lenses. High plus lenses produce “pincushion” distortion, and high minus lenses result in “barrel” distortion.
V. The Eye as an Optical Instrument
The analogy of the eye and the camera is a useful one. The focusing elements of the eye are the cornea and the crystalline lens,
and the “film” is the retina. To simplify discussions of the eye as an optical instrument, we use some approximations and resort to the schematic or reduced eye, wherein all light rays are assumed to be paraxial and all elements perfectly aligned on the visual axis.
and the “film” is the retina. To simplify discussions of the eye as an optical instrument, we use some approximations and resort to the schematic or reduced eye, wherein all light rays are assumed to be paraxial and all elements perfectly aligned on the visual axis.
The cornea contributes approximately two-thirds of the refracting power of the eye. This is true because more deflection of light rays occurs at the air-cornea interface because of the large difference in index of refraction between these two media. The crystalline lens is in fact a more powerful refracting lens than the cornea in air because it is biconvex and each of its surfaces is more convex than the cornea. The lens, however, is in the aqueous–vitreous medium, and the difference in refractive index at the aqueous–lens and lens–vitreous interfaces is much less. The cornea has an index of refraction of 1.376 and contributes +43 D to the eye.
The crystalline lens has an index of refraction that increases from the cortex to the nucleus, but averages 1.41 with a power of +20 D. Because these two refracting elements are separated, the total power of the eye is not their sum but the equivalent power of +58.7 D.
The pupil is also a significant component of the eye’s optical system. It can constrict, reducing the amount of light that enters the eye, decreasing aberrations, and increasing the eye’s depth of focus. This accounts for the ability of many people who require glasses to get along without them when the illumination is good.
The retina is a unique kind of film. It contains the “coarse grain” but highly sensitive rods for registering images at very low levels of illumination and the “fine grain” color-sensitive cones for high resolution and discrimination at high levels of illumination. Only one or two quanta of light energy are required to activate the rods. On the other hand, rapid neural adaptation and the more gradual process of adjusting the steady state between bleaching and regeneration of retinal visual pigments enable the retina to function perfectly at extremely high levels of illumination. What other film functions so well both in moonlight and at high noon? The manner in which visual images are formed, transmitted to the visual cortex, and interpreted is a fascinating story but not appropriate to this discussion.
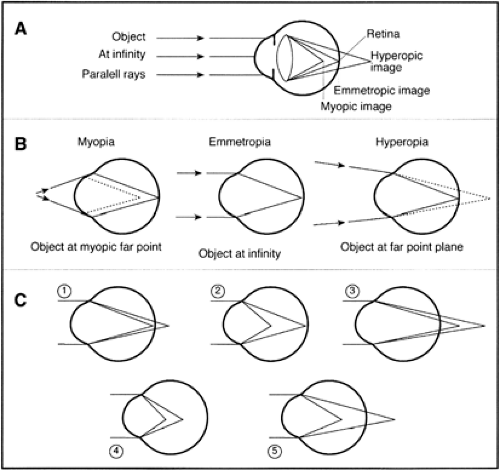
VI. Refractive Errors of the Eye (Fig. 14.4)
Emmetropia. The eye is considered to be emmetropic if parallel light rays from an object more than 6 m away are focused at the plane of the retina when the eye is in a completely relaxed state. An emmetropic eye will have a clear image of a distant object without any internal adjustment of its optics. Although most emmetropic rays are approximately 24 mm in length, a larger eye can be emmetropic if its optical components are weaker, and a smaller eye can be emmetropic if its optical components are stronger.
Ametropias
Hyperopia. When the focused image is formed behind the plane of the retina in ametropia, the eye is “too short” and is considered hyperopic. This is also referred to as farsightedness. Near images can be blurred unless there is sufficient accommodation, as in a child. Unless the optical system of the eye is actively altered to produce an increase in its power, hyperopic eyes will have blurred images for distant objects also, as any elderly hyperope will confirm. Most children are born about +3 D hyperopic, but this usually resolves by age 12 years.
Structural hyperopia is based on the anatomic configuration of the eye.
In axial hyperopia, the eye is shorter than normal in its anteroposterior (AP) diameter, although the refracting portions (e.g., lens, cornea) are normal. These eyes are more prone to develop angle-closure glaucoma because of the shorter anterior segment with crowding of the filtration angle. The optic nerves are also smaller and more densely packed, because they are crowded at the disk. Physiologic cupping is uncommon, and pseudopapilledema may be noted. The latter is seen in eyes with greater than +4 D of hyperopia, a normal blind spot on field testing, no venous congestion, and a disk that seems “swollen.”
Curvature hyperopia results when either the crystalline lens or the cornea has a weaker than normal curvature and consequently lower refractive power.
Index of refraction hyperopia is the result of decreased index of refraction due to decreased density in some or several parts of the optic system of the eye, thus lowering the refractive power of the eye.
Accommodation in hyperopia is of greater importance than the structural factors leading to it because accommodation is a key dynamic factor in correcting at least part of the refractive error. It is defined as latent, manifest facultative, and manifest absolute hyperopia.
Latent hyperopia is that part of the refractive error completely corrected by accommodation. It is measurable not by manifest refraction but only with paralysis of accommodation via cycloplegic refraction. Latent hyperopia is the difference in measurement between manifest hyperopia and the results of the cycloplegic refraction, which reveals total hyperopia, latent and manifest.
Manifest facultative hyperopia is that portion of hyperopia that may be corrected by the patient’s own powers of accommodation, by corrective lenses, or both. Vision is normal with or without corrective plus lenses, but accommodation is not relaxed without the glasses.
The effect of aging on hyperopia results from progressive loss of accommodative power, thus moving the eye from latent and facultative hyperopia to greater degrees of absolute hyperopia.
Symptoms of hyperopia
Frontal headaches worsening as the day progresses and aggravated by prolonged use of near vision.
“Uncomfortable” vision (asthenopia) when the patient must focus at a fixed distance for prolonged periods (e.g., a televised baseball game). Accommodation tires more quickly when held in a fixed level of tension.
Blurred distance vision with refractive errors greater than 3 to 4 D or in older patients with decreasing amplitude of accommodation.
Near visual acuity blurs at a younger age than in the emmetrope (e.g., in the late 30s). This is aggravated when the patient is tired, print is indistinct, or lighting conditions are suboptimal.
Light sensitivity (photophobia) is common in hyperopes, is of unknown etiology, and is relieved by correcting the hyperopia without needing to tint the lenses.
Intermittent sudden blurring of vision is due to a quick change in or spasm of accommodation. A shift toward myopia is present (pseudomyopia), and vision temporarily clears with minus lenses. The accommodative spasm may be detected by cycloplegic refraction, which will reveal the underlying hyperopia.
“Crossed-eyes” sensation without diplopia is also due to excessive accommodation in a patient with an esophoria that is being pushed by the accommodation–convergence reflex into a symptom-producing state that “the eyes are crossing.”
Treatment of hyperopia is usually most satisfactory when slightly less power (1 D) than the total of facultative and absolute hyperopia is given to a patient with no extraocular muscle imbalance. If an accommodative esotropia (convergence) is present, then the full correction should be given. In exophoria, the hyperopia should be undercorrected by 1 to 2 D. If the total manifest refractive error is small (e.g., 1 D or less), correction is given only if the patient is symptomatic.
Myopia. When the focused image is formed in front of the plane of the retina in ametropia, the eye is “too long” and is considered myopic. This is referred to as nearsightedness, because there is a point less than 6 m in front of the eye that will be coincident with the retina when the optical system of the eye is relaxed.
Types of myopia
In axial myopia, the AP diameter of the eye is longer than normal, although the corneal and lens curvatures are normal and the lens is in the normal anatomic position. In this form of myopia may be found pseudoproptosis resulting from the abnormally large anterior segment, a peripapillary myopic crescent from an exaggerated scleral ring, and a posterior staphyloma.
In curvature myopia the eye has a normal AP diameter, but the curvature of the cornea is steeper than average (e.g., congenitally or in keratoconus), or the lens curvature is increased as in moderate to severe hyperglycemia, which causes lens intumescence.
Increased index of refraction in the lens due to onset of early to moderate nuclear sclerotic cataracts is a common cause of myopia in the elderly. The sclerotic change increases the index of refraction, thus making the eye myopic. Many people find themselves ultimately able to read without glasses or having gained “second sight.” They may usually be given
normal distance vision for years simply by increasing the minus power in their corrective lenses, thus avoiding surgery.
Anterior movement of the lens is often seen after glaucoma surgery and will increase the myopic error in the eye.
Clinical course. Myopia is rarely present at birth, but often begins to develop as the child grows. It is usually detected by age 9 or 10 years in the school vision tests and will increase during the years of growth until stabilizing around the mid-teens, usually at about 5 D or less.
Pathological (progressive) myopia is a rare form of myopia that increases by as much as 4 D yearly and is associated with vitreous floaters, liquefaction, and chorioretinal changes. The refractive changes usually stabilize at about age 20 years but occasionally may progress until the mid-30s and frequently result in degrees of myopia of 10 to 20 D.
Congenital high myopia is usually a refractive error of 10 D or greater and is detected in infants who seem to be unaware of a visual world beyond their immediate surroundings, but who, fortunately, usually develop normal vision focusing on small objects held an inch or two from their eyes. This myopia is not generally progressive, but should be corrected as soon as discovered to help the child develop normal distance vision and perception of the world.
Symptoms of myopia
Blurred distance vision.
Squinting to sharpen distance vision by attempting a pinhole effect through narrowing of the palpebral fissures.
Headaches are rare but may be seen in patients with uncorrected low myopic errors.
Treatment of myopia
Children should be fully corrected and, if under 8 years of age, instructed to wear their glasses constantly both to avoid developing the habit of squinting and to enhance developing a normal accommodation-convergence reflex (see Section VI.B.5). If the refractive error is low, the child may wear the glasses intermittently as needed, (e.g., at school).
Adults under the age of 30 years are usually comfortable with their full myopic correction. Patients older than 30 years may not be able to tolerate a full correction over 3 D if they have never worn glasses before and may prefer a less than full correction, with resulting undercorrected distance vision but clear reading vision. The patient should be told that full correction might be given in the future if desired. Wearing full correction in a trial frame for about 30 minutes, with the patient both reading and looking at distance in the waiting room, may answer the question of whether to give full correction.
Undercorrection of myopia in childhood may result in an adult who has never developed a normal amount of accommodation for near focus. This person will be uncomfortable in full correction and complain that the glasses are too strong and “pull” his or her eyes.