Purpose
To investigate the vascular appearance of choroidal neovascularization (CNV) treated with recurrent intravitreous anti–vascular endothelial growth factor (VEGF) injections, which have been proposed to cause transient vascular normalization along with decreased vascularity and leakage.
Design
Retrospective case series with perspective on the topic.
Methods
Patients with treated CNV secondary to age-related macular degeneration from a community-based retinal referral practice were evaluated with optical coherence tomography angiography employing split-spectrum amplitude decorrelation. The choroidal neovascular morphology of the 17 eyes of 14 consecutive patients was described.
Results
The mean age of the patients, 8 men and 6 women, was 78.4 (standard deviation ± 9.3) years. The mean greatest linear dimension of the lesion was 3600 μm. The mean number of anti-VEGF injections was 47 (±21). The vascular diameter of the vessels in the CNV appeared large even in small lesions, with feeder vessels approaching the size of the major arcade vessels of the retina. The vessels had few branch points and many vascular anastomotic connections among larger vessels. There was a paucity of capillaries visualized within the lesions.
Conclusions
The findings of this study do not support the hypothesis of vascular normalization in eyes receiving recurrent periodic antiangiogenic treatment. The observed “abnormalization” of the vessels may be explained by periodic pruning of angiogenic vascular sprouts by VEGF withdrawal in the face of unimpeded arteriogenesis. As the eye is a readily accessible VEGF laboratory, features expressed therein may also apply to neovascularization elsewhere in the body, such as in tumors.
Organisms employ several different strategies to grow and maintain blood vessels to deliver proper amounts of oxygen and metabolites to tissue, as well as to remove wastes produced by metabolism. The mechanisms used to create new vascular networks include vasculogenesis, a term used to denote the formation of vessels de novo from endothelial precursor cells; angiogenesis, the formation of new capillaries from preexisting vessels; and arteriogenesis, which is the expansion of previously formed channels into larger vessels. While the modes of vessel formation and development may seem to be specific names given to a seamless gradation of vessel proliferation, there are significant differences in how this occurs and what causes each of these changes. Therefore there are potential features that could be targeted in preventing progression in diseases in which vessel growth is a significant feature, such as neovascular age-related macular degeneration (AMD).
A principal configuration in which neovascular AMD appears is as a fibrovascular pigment epithelial detachment (PED). The newly growing vessels elevate the retinal pigment epithelium (RPE) by their physical presence, exudation, bleeding, and any associated fibrotic proliferation. Fluid leaks from the vessels and can accumulate either below or above the RPE monolayer or within the retina. Intravitreous treatment with anti–vascular endothelial growth factor (VEGF) agents may cause a reduction of the fluid leakage, but it is common to see persistence of fluid despite treatment. Patients require monthly treatment, or at least frequent follow-up and recurrent treatment, to optimize visual outcome. Signs of exudation from neovascularization quickly return even though anti-VEGF agents decrease both angiogenesis and vascular leakage. The appearance and physiology of vessels in treated fibrovascular PEDs is largely unknown, but may have bearing on the need for chronic, frequent treatment. Introduction of the basic concepts of vascular development and morphology in health and disease will be presented prior to shifting to the findings specific to treated choroidal neovascularization (CNV).
Angiogenesis
The sprouting of vascular endothelial cells to form new vessels from preexisting vessels is chiefly stimulated by VEGF, along with a host of minor players ( Figure 1 ). Vascular endothelial cells and their mural cells have a common basement membrane. Under the influence of proangiogenic cytokines the mural cells detach and matrix metalloproteinases are released to break down the basement membrane. Interactions between Notch activity and the endothelial cells help in the selection of some of the endothelial cells to become tip cells, which lead the neovascular vanguard. The tip cells laterally inhibit neighboring endothelial cells from being tip cells; instead, they become what are known as stalk cells. The tip cells migrate in the direction of the VEGF gradient and help lead the proliferating stalk cells. Tip cell fusion initiates anastomosis with neighboring vascular outgrowths as mediated by vascular endothelial cadherin, also called VE-cadherin. The stalk cells establish a lumen and create a basement membrane, and perfusion begins. Vessel maturation is marked by reduced proliferation of endothelial cells, pericyte recruitment, pericyte maturation, and increased formation of cell junctions. Vessel maturation depends on a number of factors, a notable one being transforming growth factor (TGF) β, which participates in mural cell proliferation and migration, as well as in deposition of extracellular matrix. Platelet-derived growth factor (PDGF) participates in the recruitment, migration, and proliferation of both pericytes and smooth muscle cells, as does the bioactive lipid sphingosine-1-phosphate. Angiopoietin-1, produced by pericytes, activates the endothelial receptor tyrosine kinase with immunoglobulin-like and EGF-like domains 1, more conveniently known as TIE1, which helps stabilize vessels, promotes pericyte adhesion, and affects vascular tight junctions.

Angiogenesis is a continued process that is elicited as needed and continues in a progressive manner until the stimulus for vessel proliferation is abated. The process of angiogenesis can be modulated or blunted by pharmacologic intervention, but the underlying stimulus may not necessarily be affected. Angiogenesis is highly VEGF dependent and targeting VEGF has been a strategy in the treatment of many diseases involving the eye, as well as diseases outside of the eye, including cancer.
Arteriogenesis
The dilation of vessels in response to high-flow states occurs as a normal process in new vessel growth and is called arteriogenesis ( Figure 2 ). At one time the processes involved in arteriogenesis were folded into those of angiogenesis, but with increased knowledge of new vessel development the differences in angiogenesis and arteriogenesis became apparent. Angiogenesis is the sprouting of new capillaries, while arteriogenesis is the dilation of preexisting channels by active proliferation and remodeling of the vessel wall. An intriguing difference is that angiogenesis is highly VEGF dependent while arteriogenesis is not VEGF dependent. Thus treatment of 1 aspect in neovascularization may not necessarily affect other aspects.

Flow through blood vessels puts various stresses on the vessel. The most important is shear stress, caused by the moving blood over the endothelial cells. Shear stress is directly related to flow and inversely related to the cube of the vessel radius. The pressure required to maintain flow causes circumferential stress on the wall of the vessel. Mechanotransducers in vascular endothelial cells are activated by increased stress. Matrix metalloproteinases are released, integrins activated, and a host of inflammatory cells are recruited to the wall of the vessel. This leads to breakdown and remodeling of the extracellular matrix within the vessel wall and expansion of the vessel. Smooth muscles cells are recruited to the vessel wall, largely through the release of PDGF.
The differing role that VEGF plays in angiogenesis as opposed to arteriogenesis is striking, but another difference, although not as categorical, is the integral involvement of the inflammatory system in arteriogenesis. The innate and adaptive immune systems appear to be needed for arteriogenesis to maximally function. Monocyte depletion in both rabbit and mouse models leads to impaired arteriogenesis, which could be restored by injection of exogenous monocytes. In particular, arteriogenesis appears to be related to M2 macrophages. Genetically CD4-or CD8-deficient mice have impaired arteriogenesis that can be restored by reconstitution with the absent lymphocyte type. Chemokines, tumor necrosis factor-α, TGF α, TGF β, interferon-γ, toll-like receptors 2 and 4, and basic fibroblastic growth factor are involved in arteriogenesis as well. If there is local tissue hypoxia, for instance, coordination would occur between new sprouts of capillaries and the eventual expansion of these capillaries into larger feeding and draining vessels. Feedback mechanisms titrate the amount of increased tissue perfusion vs the reduction in the local tissue hypoxia.
Arteriogenesis
The dilation of vessels in response to high-flow states occurs as a normal process in new vessel growth and is called arteriogenesis ( Figure 2 ). At one time the processes involved in arteriogenesis were folded into those of angiogenesis, but with increased knowledge of new vessel development the differences in angiogenesis and arteriogenesis became apparent. Angiogenesis is the sprouting of new capillaries, while arteriogenesis is the dilation of preexisting channels by active proliferation and remodeling of the vessel wall. An intriguing difference is that angiogenesis is highly VEGF dependent while arteriogenesis is not VEGF dependent. Thus treatment of 1 aspect in neovascularization may not necessarily affect other aspects.
Flow through blood vessels puts various stresses on the vessel. The most important is shear stress, caused by the moving blood over the endothelial cells. Shear stress is directly related to flow and inversely related to the cube of the vessel radius. The pressure required to maintain flow causes circumferential stress on the wall of the vessel. Mechanotransducers in vascular endothelial cells are activated by increased stress. Matrix metalloproteinases are released, integrins activated, and a host of inflammatory cells are recruited to the wall of the vessel. This leads to breakdown and remodeling of the extracellular matrix within the vessel wall and expansion of the vessel. Smooth muscles cells are recruited to the vessel wall, largely through the release of PDGF.
The differing role that VEGF plays in angiogenesis as opposed to arteriogenesis is striking, but another difference, although not as categorical, is the integral involvement of the inflammatory system in arteriogenesis. The innate and adaptive immune systems appear to be needed for arteriogenesis to maximally function. Monocyte depletion in both rabbit and mouse models leads to impaired arteriogenesis, which could be restored by injection of exogenous monocytes. In particular, arteriogenesis appears to be related to M2 macrophages. Genetically CD4-or CD8-deficient mice have impaired arteriogenesis that can be restored by reconstitution with the absent lymphocyte type. Chemokines, tumor necrosis factor-α, TGF α, TGF β, interferon-γ, toll-like receptors 2 and 4, and basic fibroblastic growth factor are involved in arteriogenesis as well. If there is local tissue hypoxia, for instance, coordination would occur between new sprouts of capillaries and the eventual expansion of these capillaries into larger feeding and draining vessels. Feedback mechanisms titrate the amount of increased tissue perfusion vs the reduction in the local tissue hypoxia.
Optimal Vascular Networks
Leonardo da Vinci made the observation in his notebooks that the branches of a tree at every stage of its height, when put together, are equal in thickness to the trunk. In a more modern way of stating this, the radius of the parent branch, r 1 , equals the sum of the radii of the daughter branches, r 2 , or r 1 = r 2 + r 2 . However, from the context of the descriptions as well as the appearance of his drawings it seems that he meant that the cross-sectional area of the parent branch equaled the cross-sectional area of the daughter branches. Thus r 1 2 = r 2 2 + r 2 2 has become to be known as da Vinci’s law of branching. Note that both daughter branches are shown as r 2 , but the branching does not have to be symmetrical.
About 3 centuries after the death of da Vinci, Jean Léonard Marie Poiseuille was born. He analyzed the flow of fluid in pipes and developed the relationship resistance = 8ηl/(πr 4 ), where η is the viscosity, l is the length, and r is the radius of the pipe. From this we see that small changes in radius have a large effect on flow. However, in a biologic system there is a cost to the organism to make and maintain blood and blood vessels. Charles Murray published a series of papers in the 1926 in which he calculated the optimum diameters of blood vessels and branching that minimized total work on the part of the organism. By analyzing the relationship between the cost of a vessel vs the flow through a vessel of any given diameter, he found the relationship r 1 3 = r 2 3 + r 2 3 as an optimum. This relationship is known as Murray’s law. Later study showed widespread application of Murray’s law to biologic systems. In plants water transport systems follow Murray’s law unless they have structural duties, such as in larger tree branches, and then the ratios can approach da Vinci’s law. In animals the branching of bronchioles is described by Murray’s law, as are blood vessels. However, the exact relationship varies from tissue to tissue. The branching of blood vessels follows a general form of r 1 x = r 2 x + r 2 x , where x can range from 2.6 to 3.2. For the retina the value of x is estimated to be 2.85 ( Figure 3 ).
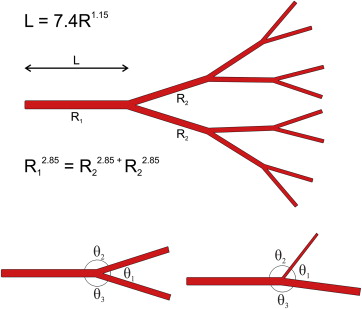
The diameter of successive branches of blood vessels follows the same modified Murray’s law and therefore, over the scale of blood vessel sizes, defines a fractal pattern. Of interest is that the segment length of any branch can be summarized as a function of its radius. For the retina the expression is l = 7.4r 1.15 , where l is the length and r is the radius. Even the branching angles of vessels can be calculated; as shown by Murray, the angles of branching are related to the relative proportions of the daughter vessel radii.
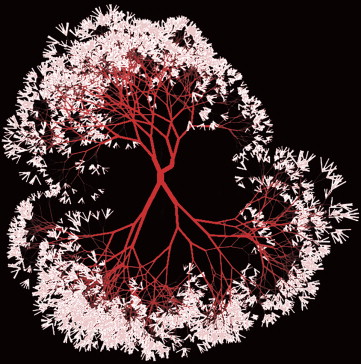
The theoretically derived values for blood vessels are based on simple goals of minimizing work, but what is the relationship between these parameters and actual vascular circuits? Sherman and associates determined that the majority of branches in a vascular circuit had energy cost functions less than 1% above the Murray minimum and the deviation for entire vascular trees departed from optimal by an average of less than 10%. Although the derivation of optimal flow characteristics has occurred recently over human history, evolutionary derivation of the same features happened much earlier. The efficiency of blood flow in cancer is much lower; Less and associates estimate that energy losses above the Murray optimum for entire trees in mammary carcinoma may be on the order of 40%–100%. While the values of the parameters undoubtedly differ by tissue and disease, if CNV grew with the same fractal parameters as do retinal vessels, a representation of the vessels could be generated; Figure 4 shows a fractal “tree” of vessels so derived. The exact format of the vascular tree in life is dependent on tissue needs, but the basic character of vessels growth and patterning shows consistency across many normal tissue types. This consistency seems to break down in local environments where the cytokine levels are presumed to be highly abnormal, such as in tumors.