Purpose
To describe a model for calculating induced stress on corneal incisions during intraocular lens implantation, and to compare the nozzles of common injectors using 2 incision sizes.
Design
Experimental study.
Methods
A finite element calculation model was developed and used to compare 7 commercially available injectors in widespread clinical use. The injectors’ characteristics were measured and correlated for the stress they induced for 2.4- or 2.2-mm corneal incisions.
Results
Each injector created a different level of stress on the corneal incision. The stress was highest at the incision margins, and its level correlated with the injector’s external circumference. The induced stress on 2.2-mm incision margins was about 9% higher compared to the induced stress on 2.4-mm incision margins.
Conclusions
A model for comparing stress induced on corneal incisions during intraocular lens implantation by 7 injectors revealed different levels of induced stress on the incision margins. It is therefore recommended that the choice of injector be matched to the size of the corneal incision.
Implantation of a foldable intraocular lens (IOL) during cataract surgery through a small incision usually requires an injector system. There have been several reports on damage to the IOLs or to the injecting system itself during the implantation process. The reported damage includes marks or scratches, stress fractures, cracks, tear lines, and deposits, as well as breaks and cracks of the cartridge nozzle. The effect of implanting an IOL through a narrow injector system on the IOL and on the injector system was previously studied, but the effect of the choice of the injector system on the corneal incision itself has not been investigated in depth.
In view of the current availability of high-quality premium IOLs and patients’ demands for perfect vision following the procedure, there is an ever-increasing need for minimizing the incision size in cataract surgery in order to reduce any surgically induced astigmatism. Smaller corneal incisions are also considered as being safer and more watertight than larger ones. There are a variety of injector systems that are commercially available. Those systems differ in their principle of action and in several of their characteristics, such as external diameter and shape of the nozzle, such that a different effect on the corneal incision can be expected from different injectors.
We developed a finite element model for the comparison of the induced stress on the corneal incision during IOL implantation according to the characteristics of the injector system. We then used the model to compare the levels of stress induced by 7 popular injector systems and 2 incision sizes; we present our findings.
Methods
This was an experimental study that did not require Institutional Review Board approval.
Finite element analysis is a commonly used method for structure behavior calculations (ie, displacements, reactions, internal loads and stresses) under various external loading and environmental conditions. The finite element analysis assumptions for our model are: (1) the model is symmetrical through both its vertical and horizontal axes; (2) the results (expressed as gr/mm 2 ) are used solely for comparison; (3) no friction exists between the cornea and the injector’s outer surface; and (4) the cut lips of the cornea are fully attached to the injector’s outer surface as a result of the cornea’s extensive flexibility.
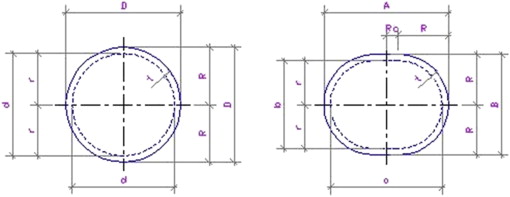
The injectors that were included in the present study were: Alcon C cartridge (Alcon, Fort Worth, Texas, USA), Alcon D cartridge (Alcon), Rayner R-INJ-04 soft tip injector (Rayner Intraocular Lenses, East Sussex, England), Rayner R-INJ-04/18 soft tip injector (Rayner), Medicel NAVIJECT 2.2 (Medicel, Wolfhalden, Switzerland), Medicel VISCOJECT 1.8 (Medicel), and MDJ 2.2 (MDJ, La Monnerie Le Montel, France). The nozzle shape of these injectors was either round or oval. Their inner and outer diameters at the tip were measured with a profile projector (H-14B NIKON, Tokyo, Japan) with a 20× magnification and a 1 micron resolution.
The cornea structure in our model was represented as a series of finite elements given the relevant geometry and material properties. The cornea finite element model was composed of 0.05 × 0.05-mm quadrant elements with 0.1 mm thickness, forming a global square model approximately 3 times the injector size in both the horizontal and vertical directions. Under these conditions, edge boundary conditions have a negligible effect on the results ( Figure 1 ). The cornea material properties were based on Young’s modulus : E = 2.45 × 10 3 kg/mm 2 .

The cornea horizontal cut was modeled as 2 series of adjacent parallel grid points disconnected vertically to allow opening during the injector penetration ( Figure 1 ). The injector penetration was simulated by using forced displacements of all cut lips grid points precisely forming (after loading) the outer surface geometry of the injector shape.
Force Displacement Calculations
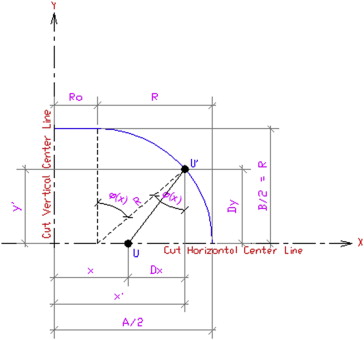
The geometrical definitions of both the round- and oval-shape injectors and the corneal incisions that were used for the forced displacement calculations are detailed in Figures 2 and 3 , respectively. The forced displacement calculations were different for the oval and round cartridges, since the oval cartridges had a straight area that was connected to the 2 hemispheres. Every grid point displacement of the round cartridges had a vertical and a horizontal component, except for the 2 margin points, which had only horizontal displacement, and the 2 grid points at the center of the incision, which had only vertical displacement. All the grid points in the oval cartridges that corresponded to the straight portion of the injectors had only vertical displacement ( Figure 4 ). A forced displacement map of the incision lips as a result of the insertion of the injector nozzles was created for each injector for both incision sizes ( Figures 5 and 6 ).


Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


